题目内容
 如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.
如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.(1)若∠A=60°,求∠A1=
(2)若∠A=m,再作∠A1BE、∠A1CE的平分线,交于点A2;再作∠A2BE、∠A2CE的平分线,交于点A3;…;依此类推,则∠An=
考点:三角形内角和定理,三角形的外角性质
专题:规律型
分析:根据“角平分线定义”和“三角形的外角等于与它不相邻的两个内角和”求出规律,直接利用规律解题.
解答:解:∵∠A1=∠A1CE-∠A1BC
=
∠ACE-
∠ABC
=
(∠ACE-∠ABC)
=
∠A.
(1)当∠A=60°时,∠A1=30°;
(2)当∠A=m时,∠A1=
m;
依此类推∠A2=
m,∠A3=
m,∠An=
.
故答案为:30;
.
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
(1)当∠A=60°时,∠A1=30°;
(2)当∠A=m时,∠A1=
| 1 |
| 2 |
依此类推∠A2=
| 1 |
| 4 |
| 1 |
| 8 |
| m |
| 2n |
故答案为:30;
| m |
| 2n |
点评:此题主要考查了三角形的内角和外角之间的关系以及角平分线的定义.三角形的外角等于与它不相邻的两个内角和.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
观察图形:将一张长方形纸片对折,可得到一条折痕.继续对折,对折是每次折痕与上次折痕保持平行,那么对折8次后折痕的条数是( )


| A、16 | B、64 |
| C、128 | D、255 |
下列方程组中,是二元一次方程组的为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
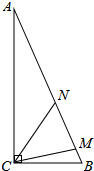 如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )
如图,在△ABC中,∠ACB=90°,AC=24,AB=25,AM=AC,BN=BC,则MN的长为( )| A、4 | B、5 | C、6 | D、7 |
已知⊙O的半径为5,点P在⊙O内,且PO=4,则过点P且弦长为整数的弦有( )条.
| A、5 | B、6 | C、7 | D、8 |
 已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.
已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.