题目内容
1.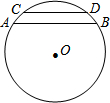 如图,⊙O的半径为5,弦AB=8,CD=6,AB∥CD且在圆心的同侧,则两条平行弦之间的距离为( )
如图,⊙O的半径为5,弦AB=8,CD=6,AB∥CD且在圆心的同侧,则两条平行弦之间的距离为( )| A. | 2 | B. | 3或4 | C. | 1 | D. | 1或7 |
分析 连接OC、OA,作直线EF⊥AB于E,交CD于F,则EF⊥CD,根据垂径定理求出CF,AE,根据勾股定理求出OE、OF,即可得出答案.
解答 解:如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,则EF⊥CD,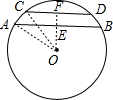
∵OE⊥AB,OF⊥CD,
∴AE=$\frac{1}{2}$AB=4,CF=$\frac{1}{2}$CD=3,
根据勾股定理,得
OE=$\sqrt{A{O}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,OF=$\sqrt{C{O}^{2}-C{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
所以当AB和CD在圆心的同侧时,则EF=OF-OE=1,
故选C.
点评 本题考查了垂径定理的知识,此题综合运用了垂径定理和勾股定理,特别注意有时要考虑两种情况.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
11.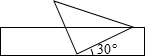 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )| A. | 2cm | B. | 4cm | C. | 2$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
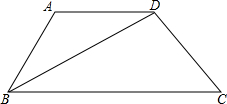 如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.
如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.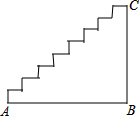 如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.
如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.