题目内容
17.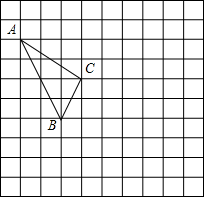 已知△ABC的顶点A(-4,5),B(-2,1),完成下列问题:
已知△ABC的顶点A(-4,5),B(-2,1),完成下列问题:(1)在如图所示的网格中建立直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′;
(3)写出点C′的坐标.
分析 (1)根据点B的坐标,向右平移2个单位,向下平移1个单位,确定出坐标原点的位置,然后以水平方向为x轴,竖直方向为y轴,建立平面直角坐标系即可;
(2)根据网格结构找出点A、B、C关于y轴的对称点A′、B′、C′的位置,然后顺次连接即可;
(3)根据网格结构即可写出点C′的坐标.
解答 解:(1)如图所示:
(2)如图,△A′B′C′就是所画的三角形;
(3)C′的坐标(1,3).
点评 本题考查了利用轴对称变换作图,平面直角坐标系的建立,根据已知点的坐标找出坐标原点的位置并建立平面直角坐标系,然后准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
8.解方程$\frac{2x+1}{3}$-$\frac{10-x}{6}$=1时,去分母正确的是( )
| A. | 2x+1-10-x=1 | B. | 4x+2-10+x=1 | C. | 4x+2-10-x=6 | D. | 4x+2-10+x=6 |
5.若分式$\frac{2+x}{{x}^{2}-4}$有意义,则x的取值范围是( )
| A. | x≠2 | B. | x≠±2 | C. | x≠-2 | D. | x≥-2 |
9.若关于x的一元一次方程ax+3x=2的解是x=1,则a的值为( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
6.以下列各组线段为边作三角形,不能构成直角三角形的是( )
| A. | 1、$\sqrt{2}$、$\sqrt{3}$ | B. | 5、12、13 | C. | 9、40、41 | D. | 2、3、4 |