题目内容
2.在长、宽、高分别为3cm,4cm,12cm的长方体盒子中分别放一木棍,木棍的最长可以为13cm.分析 根据题意画出图形,再两次运用勾股定理:两直角边的平方和等于斜边的平方进行解答即可.
解答 解:如图所示:
BC=3cm,CD=4cm,AB=12cm,
连接BD、AD,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=5(cm),
在Rt△ABD中,AD=$\sqrt{A{B}^{2}+B{D}^{2}}$=13(cm).
故这个盒子最长能放13cm的棍子.
故答案为:13cm.
点评 本题考查的是勾股定理的应用,根据题意画出图形,作出辅助线、构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
12.下列方程中,关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | x2+2x-1=0 | D. | x2+2x=x2-1 |
17.在数轴上满足-$\sqrt{3}$和$\sqrt{5}$的两点之间的距离公式是( )
| A. | $\sqrt{3}$-$\sqrt{5}$ | B. | $\sqrt{3}$+$\sqrt{5}$ | C. | $\sqrt{5}$-$\sqrt{3}$ | D. | -($\sqrt{3}$+$\sqrt{5}$) |
7.甲乙两地的海拔高度分别为300米,-50米,那么甲地比乙地高出( )
| A. | 350米 | B. | 50米 | C. | 300米 | D. | 200米 |
11.某种服装进价120元,在试销阶段发现每件售价(元)与产品的日销量(件)始终存在下表中的数量关系:
(1)根据上表所给的数据可知表中的a值是1件.
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
| 每件售价(元) | 130 | 150 | 165 | 199 |
| 每日销售量(件) | 70 | 50 | 35 | a |
(2)在不改变上述关系的情况下,当每件定价为多少元时日盈利可达1600元?
 如图,点D在AC上,且AD=CD,要使△ABC≌△ABD,可补充的一个条件是:∠CAB=∠DAB(写一个即可).
如图,点D在AC上,且AD=CD,要使△ABC≌△ABD,可补充的一个条件是:∠CAB=∠DAB(写一个即可).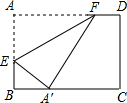 如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.
如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.