题目内容
7.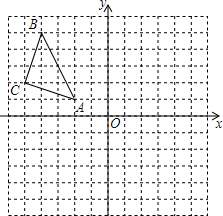 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).(1)作△ABC关于y对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1(不要求写作法);
(2)写出点A1、B1、C1的坐标.
(3)计算△A1B1C1的面积.
分析 (1)分别作出各点关于y轴的对称点,再顺次连接即可;
(2)根据各点在坐标系中的位置写出各点坐标即可;
(3)利用矩形的面积减去三个顶点上三角形的面积即可.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)由图可知,A1(2,1),B1(4,5),C1(5,2);
(3)S△A1B1C1=3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4
=12-$\frac{3}{2}$-$\frac{3}{2}$-4
=12-3-4
=5.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
17.在数轴上满足-$\sqrt{3}$和$\sqrt{5}$的两点之间的距离公式是( )
| A. | $\sqrt{3}$-$\sqrt{5}$ | B. | $\sqrt{3}$+$\sqrt{5}$ | C. | $\sqrt{5}$-$\sqrt{3}$ | D. | -($\sqrt{3}$+$\sqrt{5}$) |
2.下面几个有理数中,最小的数是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | $\frac{1}{6}$ |
16.下列关于x的方程中,一定是一元二次方程的为( )
| A. | x2-1=0 | B. | x2+2y+1=0 | C. | x2-2=(x+3)2 | D. | x2$+\frac{3}{x}-5=0$ |
 如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,求∠CAE的度数.
如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,求∠CAE的度数. 如图,DE与BC不平行,请添加一个条件:∠ADE=∠C(答案不唯一),使△ADE∽△ACB.
如图,DE与BC不平行,请添加一个条件:∠ADE=∠C(答案不唯一),使△ADE∽△ACB.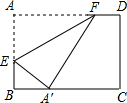 如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.
如图,长方形ABCD中,AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′在线段BC上可移动的最大距离是4.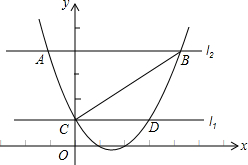 如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴交于点C,直线l1经过点C且平行于x轴,将直线l1向上平移t个单位得到直线l2,设直线l1与抛物线F的交点为C、D,直线l2与抛物线F的交点为A、B,连接AC、BC.