Question

5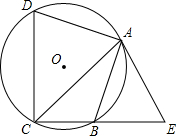．如图，四边形ABCD内接于⊙O，点E在CB的延长线上，连接AC，AE，∠ACB=∠BAE=45°
（1）求证：AE是⊙O的切线；
（2）若 AB=AD，AC=2$\sqrt{2}$，tan∠ADC=3，求CD的长．

Answer 1

分析 （1）连接OA、OB，由圆周角定理得出∠AOB=2∠ACB=90°，由等腰直角三角形的性质得出∠OAB=∠OBA=45°，求出∠OAE=∠OAB+∠BAE=90°，即可得出结论；
（2）作AF⊥CD于F，证出$\widehat{AB}=\widehat{AD}$，由圆周角定理得出∠ACB=∠ACD=45°，由三角函数求出AF=CF=AC•sin∠ACF=2，DF=$\frac{2}{3}$，即可得出CD的长．

解答 （1）证明：连接OA、OB，如图1所示：
∵∠ACB=45°，
∴∠AOB=2∠ACB=90°，
∵OA=OB，
∴∠OAB=∠OBA=45°，
∵∠BAE=45°，
∴∠OAE=∠OAB+∠BAE=90°，
∴AE⊥OA，
∴AE是⊙O的切线；
（2）解：作AF⊥CD于F，如图2所示：
∵AB=AD，
∴$\widehat{AB}=\widehat{AD}$，
∴∠ACB=∠ACD=45°，
∵AF⊥CD，
∴∠AFC=∠AFD=90°，
∵AC=2$\sqrt{2}$，
∴在Rt△AFC中，AF=CF=AC•sin∠ACF=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2，
∵在Rt△AFD中，tan∠ADC=$\frac{AF}{DF}$=3，
∴DF=$\frac{2}{3}$，
∴CD=CF+DF=2+$\frac{2}{3}$=$\frac{8}{3}$．

点评 本题考查了切线的判定、圆周角定理、等腰直角三角形的性质、三角函数等知识；熟练掌握切线的判定，由三角函数求出AF和DF是解决问题（2）的关键．