题目内容
15. 如图,己知点B,D在AC的两侧,E,F分别是△ACD与△ABC的重心,且EF=2,则BD的长度是( )
如图,己知点B,D在AC的两侧,E,F分别是△ACD与△ABC的重心,且EF=2,则BD的长度是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 连接DE并延长,交AC于点O,连接BO.根据重心的性质得出FB=2FO,ED=2EO,再证明△EOF∽△DOB,根据相似三角形对应边成比例求出BD=3EF=6.
解答  解:如图,连接DE并延长,交AC于点O,连接BO.
解:如图,连接DE并延长,交AC于点O,连接BO.
∵点E为△ADC的重心,
∴点O为AC的中点,FB=2FO;
又∵点F为△ABC的重心,
∴点F在线段BO上,ED=2EO;
∴$\frac{OF}{OB}$=$\frac{OE}{OD}$=$\frac{1}{3}$,
又∵∠EOF=∠DOB,
∴△EOF∽△DOB,
∴$\frac{EF}{BD}$=$\frac{OF}{OB}$=$\frac{OE}{OD}$=$\frac{1}{3}$,
∴BD=3EF=6.
故选C.
点评 本题主要考查了三角形的重心及其应用问题;解题的关键是作辅助线,灵活运用三角形重心的性质及相似三角形的判定与性质来解题.

练习册系列答案
相关题目
7.在$\sqrt{16{x}^{3}}$、-$\frac{\sqrt{5}}{3}$、$\sqrt{0.5}$、$\sqrt{\frac{a}{x}}$、$\sqrt{20}$中,最简二次根式的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.$\root{3}{-64}$的绝对值是( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
 如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥C,交AC的延长线于点E.
如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥C,交AC的延长线于点E.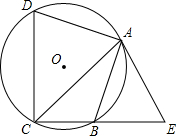 如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°
如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°