题目内容
19.已知抛物线y=(m-1)x2-2mx+m+1(m>1).(1)求抛物线与x轴的交点坐标;
(2)若抛物线与x轴的两个交点之间的距离为2,求m的值.
分析 (1)令y=0得;(m-1)x2-2mx+m+1=0,然后求得△=4,最后利用一元二次方程的求根公式求得方程的解,从而得到抛物线与x轴的交点坐标;
(2)根据两个交点之间的距离为2,列出关于m的方程,从而可解得m的值.
解答 解:(1)令y=0得;(m-1)x2-2mx+m+1=0.
△=b2-4ac=(-2m)2-4(m-1)(m+1)=4.
∴${x}_{1}=\frac{2m+2}{2(m-1)}$=$\frac{m+1}{m-1}$,x2=$\frac{2m-2}{2(m-1)}=1$.
∴抛物线与x轴交点坐标为($\frac{m+1}{m-1}$,0)、(1,0).
(2)∵m>1,
∴$\frac{m+1}{m-1}$>0.
∵两个交点之间的距离为2,
∴$\frac{m+1}{m-1}$-1=2.
解得:m=2.
∵当m=2时,m-1≠0,
∴m=2是分式方程的解.
∴m的值为2.
点评 本题主要考查的是抛物线与x轴的交点问题,利用一元二次方程的求根公式求得方程的两根是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
10.若关于x的一元二次方程(m-1)x2-2x+1=0有两个不相等的实数根,则m的取值范围是( )
| A. | m<2且m≠1 | B. | m>2 | C. | m<-2 | D. | m<2 |
7. 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )| A. | 4 | B. | -4 | C. | ±4 | D. | -5 |
11.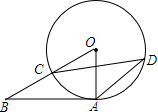 如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
 如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )
如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是( )| A. | 27° | B. | 34° | C. | 36° | D. | 54° |
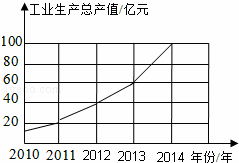 如图是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图可得:增长幅度最大的年份是2014年,比它的前一年增加40亿元.
如图是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图可得:增长幅度最大的年份是2014年,比它的前一年增加40亿元.