题目内容
7.在形如ab=N的式子中,我们已经研究过两种情况:已知a和b求N,这是乘方运算:已知b和N求a,这是开方运算,现在我们研究第三种情况:已知a和N求b,我们称这种运算为对数运算.定义:如果23=8,所以log28=3:因为32=9,所以log39=2
根据以上信息回答下列问题:
(1)计算:log381=4,log33=1,log636=2,logx16=4,则x=2.
(2)设ax=M,ay=N(a>0,且a≠1,M>0,N>0),猜想logaMN和loga$\frac{M}{N}$的结果,并证明.
(3)计算:①log2(2×4×8×16×32×64);②log3$\frac{243}{81}$;③log93+log927.
分析 (1)利用题中的新定义求出所求式子的值即可;
(2)猜想logaMN=x+y;loga$\frac{M}{N}$=x-y,利用新定义证明即可;
(3)各式利用新定义计算即可得到结果.
解答 解:(1)log381=log334=4,log33=1,log636=log662=2,logx16=4,则x=2;
故答案为:4;1;2;2;
(2)logaMN=logaM+logaN;loga$\frac{M}{N}$=logaM-logaN;
证明:logaMN=logaax•ay=logaax+y=x+y;logaM+logaN=x+y,
则logaMN=logaM+logaN;
loga$\frac{M}{N}$=loga$\frac{{a}^{x}}{{a}^{y}}$=logaax-y=x-y;logaM-logaN=x-y,
则loga$\frac{M}{N}$=logaM-logaN;
(3)①原式=log22+log24+log28+log216+log232+log264=1+2+3+4+5+6=21;
②原式=log3243-log381=5-4=1;
③原式=log93×27=log981=2.
点评 此题考查了整式的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.-23÷(-4)的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
2.下列计算错误的是( )
| A. | x+x2=x3 | B. | x•x2=x3 | C. | x5÷x2=x3 | D. | (x2)3=x6 |
16. 如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
 如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )
如图,两条宽为1的带子,相交成α角,那么重叠部分的面积即阴影部分的面积为( )| A. | sinα | B. | $\frac{1}{sinα}$ | C. | $\frac{1}{si{n}^{2}α}$ | D. | $\frac{1}{cosα}$ |
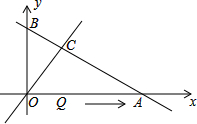 如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.
如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.