题目内容
12.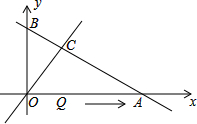 如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.
如图,直线y=-$\frac{1}{2}$x+3与坐标轴分别交于点A、B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连接CQ.若△OQC是等腰直角三角形,则t的值为2或4.
分析 分为两种情况,画出图形,根据等腰三角形的性质求出即可.
解答  解:∵由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
解:∵由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴C(2,2);
如图1,当∠CQO=90°,CQ=OQ,
∵C(2,2),
∴OQ=CQ=2,
∴t=2,
②如图2,当∠OCQ=90°,OC=CQ,
过C作CM⊥OA于M,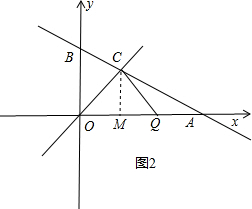
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴t=2+2=4,
即t的值为2或4,
故答案为:2或4;
点评 本题考查了用待定系数法求出一次函数解析式,等腰直角三角形等知识点的应用,题目是一道比较典型的题目,综合性比较强.

练习册系列答案
相关题目
17.已知5个正数a,b,c,d,e,且a<b<c<d<e,则新一组数据0,a,b,c,d,e的中位数是( )
| A. | b | B. | c | C. | $\frac{c+d}{2}$ | D. | $\frac{b+c}{2}$ |
2.计算$\sqrt{\frac{2}{3}}$÷$\sqrt{\frac{3}{2}}$的结果是( )
| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{2}{3}$ |
 如图,已知△ABC,求作:∠A的平分线,BC边上中线,并标上字母(要求用尺规作图,不写作法,但要保留作图痕迹).
如图,已知△ABC,求作:∠A的平分线,BC边上中线,并标上字母(要求用尺规作图,不写作法,但要保留作图痕迹).