题目内容
4．计算：$\sqrt{16}$+（-$\frac{1}{2}$）-1+（$\sqrt{3}$+5）0-$\sqrt{3}$tan30°．分析 分别利用算术平方根以及负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值化简求出即可．
解答 解：原式=4-2+1-$\sqrt{3}×\frac{{\sqrt{3}}}{3}$
=4-2+1-1
=2．
点评 此题主要考查了算术平方根以及负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值等知识，正确化简各数是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
10．下列各数中，最小的数是（ ）
| A． | -3 | B． | |-2| | C． | （-3）2 | D． | 2×103 |
7．已知a=$\frac{{\sqrt{2}}}{2}$，b=$\frac{{\sqrt{3}}}{3}$，c=$\frac{{\sqrt{5}}}{5}$，则下列大小关系正确的是（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | b＞a＞c | D． | a＞c＞b |
9．在平面直角坐标系中，点（4，-5）关于x轴对称点的坐标为（ ）
| A． | （4，5） | B． | （-4，-5） | C． | （-4，5） | D． | （5，4） |
16．下列各数中，最小的数是（ ）
| A． | 3-2 | B． | $\frac{2}{5}$ | C． | 1-$\frac{1}{7}$ | D． | $\sqrt{2}$ |
13．不等式组$\left\{\begin{array}{l}\frac{x-3}{2}+3≥x+1\\ 1-3（x-1）＜8-x\end{array}\right.$的整数解是（ ）
| A． | -2，-1，0 | B． | -1，0，1 | C． | 0，1，2 | D． | 1，2，3 |
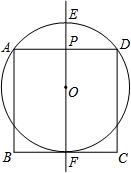在正方形ABCD中，AD=2，l是过AD中点P的一条直线．O是l上一点，以O为圆心的圆经过点A、D，直线l与⊙O交于点E、F（E、F不与A、D重合，E在F的上面）．