题目内容
8.在△ABC中,∠A=48°,∠B=42°,则△ABC的形状是( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 无法确定 |
分析 由三角形内角和等于180°及∠A、∠B的度数,可以求出∠C的度数,根据三个角的度数,可以判定三角形的形状.
解答 解:∵∠A+∠B+∠C=180°,∠A=48°,∠B=42°,
∴∠C=180°-∠A-∠B=180°-48°-42°=90°,
∴△ABC是直角三角形;
故选C.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
19.下列方程中,是一元二次方程的是( )
| A. | x2=0 | B. | ax2+bx+c=0(a,b,c均为常数) | ||
| C. | x2+y=5 | D. | x3+$\frac{2}{x}$+1=0 |
16.已知$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$≠0,则$\frac{c-a}{b}$的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
13.对下列问题进行调查时采用的方式适合普查的是( )
| A. | 工厂对准备出厂的一批轿车的刹车系统进行测试 | |
| B. | 对某市九年级学生的视力调查 | |
| C. | 某质检部门调查某罐头厂生产的一批罐头的质量 | |
| D. | 对某厂生产的摩托车头盔进行防撞击性能测试 |
20.多项式-$\frac{1}{4}$x2+x-1的值一定是( )
| A. | 正数 | B. | 负数 | C. | 不可能为负数 | D. | 不可能为正数 |
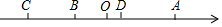 如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.
如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.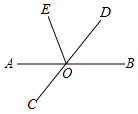 如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.
如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.