题目内容
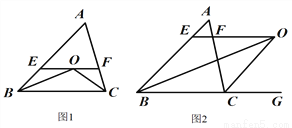
已知,如图1:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)直接写出图1中所有的等腰三角形,并指出EF与BE、CF间有怎样的数量关系?
(2)在(1)的条件下,若AB=10,AC=15,求△AEF的周长.
(3)如图2,若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F,请问(1)中EF与BE、CF间的关系还是否存在,若存在,说明理由;若不存在,写出三者新的数量关系,并说明理由.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


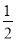 ;
;
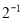 +|﹣
+|﹣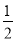 |+(
|+(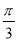 )0
)0