题目内容
16.某瓶中装有1分,2分,5分三种硬币,15枚硬币共3角5分,则有多少种装法( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设1分,2分硬币分别为x枚和y枚,则5分硬币为15-x-y,根据15枚硬币共3角5分,得到方程x+2y+5(15-x-y)=35,进而得出x=10-$\frac{3}{4}$y,据此可得可能的装法.
解答 解:设1分,2分硬币分别为x枚和y枚,则5分硬币为15-x-y,依题意得
x+2y+5(15-x-y)=35,
∴x=10-$\frac{3}{4}$y,
当y=4时,x=7,15-x-y=4;
当y=8时,x=4,15-x-y=3;
当y=12时,x=1,15-x-y=2;
故有3种装法,
故选:C.
点评 本题主要考查了二元一次方程的应用,解决问题的关键是根据二元一次方程求得方程的正整数解.

练习册系列答案
相关题目
7.下列语句错误的是( )
| A. | 连接两点的线段的长度叫做这两点间的距离 | |
| B. | 两直线平行,同旁内角互补 | |
| C. | 若两个角有公共顶点且有一条公共边,和等于平角,则这两个角互为邻补角 | |
| D. | 平移变换中,连接各组对应点所得线段平行且相等 |
4.A地在河的上游,B地在河的下游,若船从A地开往B地速度为v1,从B地返回A地的速度为v2,则A、B两地间往返一次的平均速度为( )
| A. | $\frac{{{v_1}+{v_2}}}{2}$ | B. | $\frac{{2\;{v_1}{v_2}}}{{{v_1}+{v_2}}}$ | C. | $\frac{2}{{{v_1}+{v_2}}}$ | D. | $\frac{{{v_1}+{v_2}}}{{2\;{v_1}{v_2}}}$ |
8.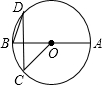 如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
 如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )
如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2$\sqrt{3}$,则∠D等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |

 如图,AB是⊙O的直径,AC是弦,D在AB的延长线上,CA=CD,∠ACD=120°,BD=10.
如图,AB是⊙O的直径,AC是弦,D在AB的延长线上,CA=CD,∠ACD=120°,BD=10.