题目内容
新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A、(2900-x)(8+4×
| ||
B、(400-x)(8+4×
| ||
C、4(2900-x)(8+
| ||
D、4(400-x)(8+
|
考点:由实际问题抽象出一元二次方程
专题:销售问题
分析:销售利润=一台冰箱的利润×销售冰箱数量,一台冰箱的利润=售价-进价,降低售价的同时,销售量就会提高,“一减一加”,根据每台的盈利×销售的件数=5000元,即可列方程.
解答:解:设每台冰箱的降价应为x元,依题意得:(400-x)(8+4×
)=5000,
故选B.
| x |
| 50 |
故选B.
点评:考查了由实际问题抽象出一元二次方程的知识,本题关键是会表示一台冰箱的利润,销售量增加的部分.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.

练习册系列答案
相关题目
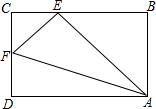 如图所示,在矩形ABCD中,E、F是BC、CD上的点,且∠AEF=90°,求证:△ABE∽△ECF.
如图所示,在矩形ABCD中,E、F是BC、CD上的点,且∠AEF=90°,求证:△ABE∽△ECF.