题目内容
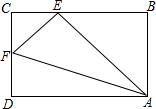 如图所示,在矩形ABCD中,E、F是BC、CD上的点,且∠AEF=90°,求证:△ABE∽△ECF.
如图所示,在矩形ABCD中,E、F是BC、CD上的点,且∠AEF=90°,求证:△ABE∽△ECF.考点:相似三角形的判定
专题:证明题
分析:由四边形ABCD是矩形,可得∠B=∠C=90°,又由∠AEF=90°,即可证得∠CEF=∠BAE,继而证得:△ABE∽△ECF.
解答:证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠CEF+∠AEB=90°,
∴∠CEF=∠BAE,
∴△ABE∽△ECF.
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠CEF+∠AEB=90°,
∴∠CEF=∠BAE,
∴△ABE∽△ECF.
点评:此题考查了相似三角形的判定以及矩形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
已知线段a=4,b=9,线段x是a,b的比例中项,则x等于( )
| A、36 | B、6 | C、-6 | D、6或-6 |
不等式(x+1)(x-2)>x(x+2)的解集是( )
A、x<
| ||
B、x<-
| ||
C、x>-
| ||
D、x>
|
新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A、(2900-x)(8+4×
| ||
B、(400-x)(8+4×
| ||
C、4(2900-x)(8+
| ||
D、4(400-x)(8+
|
以下关于-
这个数在数轴上的位置的描述,其中正确的是( )
| 3 |
| 2 |
| A、在-3的左边 |
| B、在3的右边 |
| C、在原点和-1之间 |
| D、在-1的左边 |
 如图,∠ACB=90°,D为AB的中点,已知CD=1cm,则AB的长为
如图,∠ACB=90°,D为AB的中点,已知CD=1cm,则AB的长为 已知等边△ABC中,D是BC边上的动点,∠EDF=60°.求证:△BDE∽△CFD.
已知等边△ABC中,D是BC边上的动点,∠EDF=60°.求证:△BDE∽△CFD.