题目内容
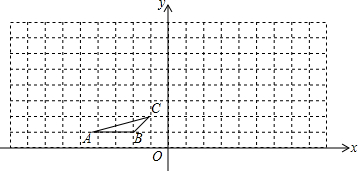
1.如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均为格点上,建立平面直角坐标系后,点A的坐标为(-4,1).(1)在图中画出△ABC关于直线x=1对称的△A1B1C1,设点P(a,b)为△ABC内的一点,直接写出点P在△A1B1C1中的对应点P1的对应P1的坐标.
(2)以原点O为D的位似中心,位似比为2,在第二象限内作△ABC的位似图形△A2B2C2,并写出C2的坐标.
分析 (1)分别写出点A、B、C关于直线x=1的对称点A1、B1、C1的坐标,然后描点得到△A1B1C1,再利用各对应点的坐标变换规律写出点P的对应P1的坐标;
(2)延长OA到OA2使OA2=2OA,则点A2为点A的对应点,同样方法画出点B、C的对应点B2、C2,从而得到△A2B2C2,然后写出C2的坐标.
解答 解:(1)如图,△A1B1C1为所作,P1的坐标为(-a+2,b);
(2)如图,△A2B2C2为所求,C2的坐标为(-2,4).
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;然后根据位似比,确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.也考查了轴对称变换.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
5.下列运算正确的是( )
| A. | a2-a=a | B. | ax+ay=axy | C. | m2•m4=m6 | D. | (y3)2=y5 |
6.下列运用等式的性质对等式进行变形,正确的是( )
| A. | 由-$\frac{x}{4}$=0,得x=4 | B. | 由x-1=3,得x=4 | C. | 由-2x=6,得x=3 | D. | 由3x=2,得x=$\frac{3}{2}$ |
13.随着世界气候大会于2009年12月在丹麦首都哥本哈根的召开,“低碳生活”概念风靡全球.在“低碳”理念的引领下,某市为实现森林城市建设的目标,在今年春季的绿化工作中,绿化办计划为某住宅小区购买并种植400株树苗,某树苗公司提供如下信息:
信息一:可供选择的树苗有雪松、香樟,垂柳三种,并要求购买雪松、香樟的数量相等.
信息二:如下表:设购买雪松,垂柳分别为x株、y株.
(1)写出y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当每株垂柳的批发价P等于30元时,要使这400株树苗两年后对该住宅小区的空气净化指数不低于90,应
怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低的总费用是多少元?
(3)当每株垂柳批发价格P(元)与购买数量y(株)之间存在关系P=30-0.05y时,求购买树苗的总费用W(元)与购买雪松数量x(株)之间的函数关系式(不要求写出自变量的取值范围),并求出购买树苗总费用的最大值.
信息一:可供选择的树苗有雪松、香樟,垂柳三种,并要求购买雪松、香樟的数量相等.
信息二:如下表:设购买雪松,垂柳分别为x株、y株.
| 树苗 | 每株树苗批发价格(元) | 两年后每株树苗对空气的净化指数 |
| 雪松 | 30 | 0.4 |
| 香樟 | 20 | 0.1 |
| 垂柳 | P | 0.2 |
(2)当每株垂柳的批发价P等于30元时,要使这400株树苗两年后对该住宅小区的空气净化指数不低于90,应
怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低的总费用是多少元?
(3)当每株垂柳批发价格P(元)与购买数量y(株)之间存在关系P=30-0.05y时,求购买树苗的总费用W(元)与购买雪松数量x(株)之间的函数关系式(不要求写出自变量的取值范围),并求出购买树苗总费用的最大值.