题目内容
20. 如图,∠1=∠2,∠3=∠4,EF⊥AD于F,求证:∠AEF=∠DEF.
如图,∠1=∠2,∠3=∠4,EF⊥AD于F,求证:∠AEF=∠DEF.
分析 由三角形的外角的性质得到∠ADE=∠1+∠4,由于∠DAE=∠2+∠3,根据已知条件得到∠ADE=∠DAE,根据等腰三角形的判定得到AE=DE,然后由等腰三角形的性质得到结论.
解答 解:∵∠ADE=∠1+∠4,∠DAE=∠2+∠3,
∵∠1=∠2,∠3=∠4,
∴∠ADE=∠DAE,
∴AE=DE,
∵EF⊥AD于F,
∴∠AEF=∠DEF.
点评 本题考查了等腰三角形的判定和性质,三角形的外角的性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2015的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | (-3)2015 |
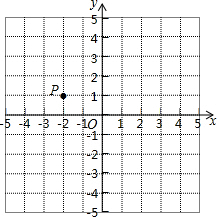 已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)
已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)  如图,△ABC的边AC与△BCD的边BD相交于点E,求证:AC+BD>AB+CD.
如图,△ABC的边AC与△BCD的边BD相交于点E,求证:AC+BD>AB+CD.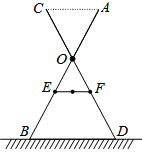 如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器)
如图是一晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32cm,求扣链EF与立杆AB的夹角∠OEF的度数.(精确到0.1°,可使用科学计算器)