题目内容
 如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.
如图,在梯形ABCD中,AD∥BC,∠DCB=90°,点E是边AB的中点,联结DE,延长DE交CB的延长线于点F,∠CBA=2∠F,且AC=BC.(1)求证:△FBE∽△EFC;
(2)求证:DC2=AD•FC.
考点:相似三角形的判定与性质,平行线的性质,直角三角形斜边上的中线
专题:证明题
分析:(1)由条件可证明△AED≌△BEF,可得E为DF的中点,由直角三角形的性质可知EF=EC,可得到∠F=∠FEB=∠ECF,可证明△FBE∽△EFC;
(2)根据(1)的过程及条件可求得∠F=∠ECF=30°,可求得∠ACD=30°,可证得△ADC∽△DCF,根据相似三角形的性质可证得结论.
(2)根据(1)的过程及条件可求得∠F=∠ECF=30°,可求得∠ACD=30°,可证得△ADC∽△DCF,根据相似三角形的性质可证得结论.
解答:证明:(1)∵AD∥BC,
∴∠ADF=∠EFB,
∵E为AB中点,
∴AE=BE,
在△AED和△BEF中,
,
∴△AED≌△BEF(AAS),
∴EF=DE,
∵∠DCB=90°,
∴CE=EF,
∴∠F=∠ECF,
∵∠CBF=2∠F,
∴∠F=∠FEB,
∴∠FEB=∠ECF,且∠F=∠F,
∴△FBE∽△EFC;
(2)∵AC=BC,E为AB中点,
∴CE⊥AB,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
又由(1)可得∠EBC=2∠ECB,
∴∠F=∠ECB=∠ECA=30°,
∵∠DCB=90°,
∴∠DCA=30°,
∴∠DCA=∠F,
又∵∠AD∥BC,
∴∠ADC+∠DCB=180°,
∴∠ADC=∠DCF=90°,
∴△ADC∽△DCF,
∴
=
,
∴DC2=AD•FC.
∴∠ADF=∠EFB,
∵E为AB中点,
∴AE=BE,
在△AED和△BEF中,
|
∴△AED≌△BEF(AAS),
∴EF=DE,
∵∠DCB=90°,
∴CE=EF,
∴∠F=∠ECF,
∵∠CBF=2∠F,
∴∠F=∠FEB,
∴∠FEB=∠ECF,且∠F=∠F,
∴△FBE∽△EFC;
(2)∵AC=BC,E为AB中点,
∴CE⊥AB,
∴∠CEB=90°,
∴∠ECB+∠EBC=90°,
又由(1)可得∠EBC=2∠ECB,
∴∠F=∠ECB=∠ECA=30°,
∵∠DCB=90°,
∴∠DCA=30°,
∴∠DCA=∠F,
又∵∠AD∥BC,
∴∠ADC+∠DCB=180°,
∴∠ADC=∠DCF=90°,
∴△ADC∽△DCF,
∴
| AD |
| DC |
| DC |
| CF |
∴DC2=AD•FC.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,即①两个三角形的两组边对应成比例且夹角相等,②两个三角形有两组角对应相等,③两个三角形的三边对应成比例,则这两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
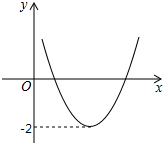 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )| A、k<2 | B、k>2 |
| C、0<k<2 | D、-2<k<2 |
 将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.
将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.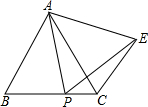 如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE. 如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G.
如图,AB是⊙O的直径,BE是弦,C是劣弧BE的中点,过C作CD⊥AB于D,CD交BE于点F,过C作CG∥BE交AB延长线于点G. 找出图中所有的同位角、内错角、同旁内角.
找出图中所有的同位角、内错角、同旁内角. 某人在河旁高4米的土堆CD的顶端D观察河对岸树AB的顶部A仰角为30°,树顶A的倒影F俯角为45°,求树高.
某人在河旁高4米的土堆CD的顶端D观察河对岸树AB的顶部A仰角为30°,树顶A的倒影F俯角为45°,求树高.