题目内容
 如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2
如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2| 3 |
考点:解直角三角形,等边三角形的性质
专题:
分析:由等边三角的性质可得:AB=BC,∠B=60°,由DE⊥AB于E,可得:∠DEB=90°,∠BDE=30°,由直角三角形中30°角所对的直角边等于斜边的一半,可得:BD=2BE,然后由勾股定理可求BE和BD的值,再由BD:CD=2:1,可求CD的长,进而确定BC的长,由AB=BC即可求出AE的长.
解答:解:∵△ABC是等边三角形,
∴AB=BC,∠B=60°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠BDE=30°,
∴BD=2BE,
在Rt△BDE中,设BE=x,则BD=2x,
∵DE=2
,
由勾股定理得:(2x)2-x2=(2
)2,
解得:x=2,
所以BE=2,BD=4,
∵BD:CD=2:1,
∴CD=2,
∴BC=BD+CD=6,
∵AB=BC,
∴AB=6,
∵AE=AB-BE
∴AE=6-2=4.
∴AB=BC,∠B=60°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠BDE=30°,
∴BD=2BE,
在Rt△BDE中,设BE=x,则BD=2x,
∵DE=2
| 3 |
由勾股定理得:(2x)2-x2=(2
| 3 |
解得:x=2,
所以BE=2,BD=4,
∵BD:CD=2:1,
∴CD=2,
∴BC=BD+CD=6,
∵AB=BC,
∴AB=6,
∵AE=AB-BE
∴AE=6-2=4.
点评:此题考查了解直角三角形,解题的关键是:利用直角三角形中30°角所对的直角边等于斜边的一半,得到:BD=2BE.

练习册系列答案
相关题目
 如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )
如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列变形错误的是( )
| A、若a=b,则5a=5b | ||||
| B、若a=b,则3-a=3-b | ||||
| C、若am=bm,则a=b | ||||
D、若
|
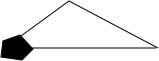 如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )
如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.