题目内容
1.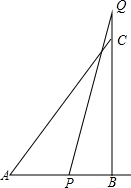 如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点A出发沿射线AB以2m/s的速度移动;同时,点Q从点C出发沿边BC的延长线以1cm/s的速度移动.
如图,在Rt△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点A出发沿射线AB以2m/s的速度移动;同时,点Q从点C出发沿边BC的延长线以1cm/s的速度移动.(1)经过多长时间P,Q两点之间的距离与AC相等?
(2)连接PC,当点P运动多长时间时,S△PCQ=$\frac{1}{2}$S△ABC?
分析 (1)设经过x秒P,Q两点之间的距离与AC相等,则PB=3-2x,BQ=4+x,利用勾股定理建立方程解答即可;
(2)设当点P运动a秒时,分两种情况PB=3-2a或PB=2a-3,CQ=a,根据三角形的面积计算公式建立方程解答即可.
解答 解:(1)设经过x秒P,Q两点之间的距离与AC相等,则PB=3-2x,BQ=4+x,由题意得
(3-2x)2+(4+x)2=32+42,
解得:x1=$\frac{4}{5}$,x2=0(舍去)
答:经过$\frac{4}{5}$秒P,Q两点之间的距离与AC相等.
(2)设当点P运动a秒时,当PB=3-2a,CQ=a时,由题意得
$\frac{1}{2}$×a(3-2a)=$\frac{1}{2}$×$\frac{1}{2}$×3×4
此方程无解.
当PB=2a-3,CQ=a时,由题意得
$\frac{1}{2}$×a(2a-3)=$\frac{1}{2}$×$\frac{1}{2}$×3×4
解得:a1=$\frac{3+\sqrt{57}}{4}$,a2=$\frac{3-\sqrt{57}}{4}$(舍去)
答:当点P运动$\frac{3+\sqrt{57}}{4}$m时,S△PCQ=$\frac{1}{2}$S△ABC.
点评 此题考查一元二次方程的实际运用,利用勾股定理和三角形的面积建立方程是解决问题的关键.

练习册系列答案
相关题目
11.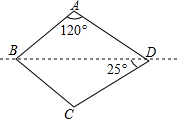 如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
 如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )
如图,直线BD是四边形ABCD的对称轴,已知∠BAD=120°,∠CDB=25°,则∠ABC的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 80° |
12.已知:a、b、c为整数,且满足${(\frac{50}{27})}^{a}$•${(\frac{18}{25})}^{b}$•${(\frac{9}{8})}^{c}$=8 试求a,b,c的值.
13.已知直角三角形的一条斜边和直角边恰为方程x2-5x+6=0的解.则此直角三角形的面积为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
11.三角形的三个外角的平分线相交所组成的图形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |