题目内容
14.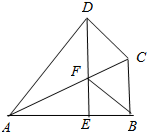 如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.
如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.
分析 由四边形ABCD是筝形,得出AB=AD,BC=CD,由SSS证明△ABC≌△ADC,得出∠ADC=∠ABC=90°,∠BAC=∠DAC,由角的互余关系和对顶角相等得出∠DCF=∠DFC,即可得出DF=CD;证出DF∥BC,DF=BC得出四边形BCDF是平行四边形,即可得出结论.
解答 证明:∵四边形ABCD是筝形,
∴AB=AD,BC=CD,
在△ABC和△ADC中,
$\left\{\begin{array}{l}{AB=AD}&{\;}\\{BC=DC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠ADC=∠ABC=90°,∠BAC=∠DAC,
∴∠DCF+∠DAC=90°,
∵DE⊥AB,
∴∠AEF=90°,∠AFE+∠BAC=90°,
∴∠DCF=∠AFE,
∵∠DFC=∠AFE,
∴∠DCF=∠DFC,
∴DF=CD;
四边形BCDF是菱形;理由如下:
∵∠ABC=∠AEF=90°,
∴DF∥BC,
∵DF=CD,BC=CD,
∴DF=BC,
∴四边形BCDF是平行四边形,
又∵DF=CD,
∴四边形BCDF是菱形.
点评 本题考查了筝形的性质、全等三角形的判定与性质、等腰三角形的判定、平行四边形的判定、菱形的判定;本题综合性强,有一定难度.

练习册系列答案
相关题目
5. 两圆有多种位置关系,图中不存在的位置关系是( )
两圆有多种位置关系,图中不存在的位置关系是( )
 两圆有多种位置关系,图中不存在的位置关系是( )
两圆有多种位置关系,图中不存在的位置关系是( )| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
2.下列函数中,y是x的正比例函数的是( )
| A. | y=2x-1 | B. | y=$\sqrt{2}$x | C. | y=2x2 | D. | y=kx |
19.某班阅读兴趣小组10名同学的年龄情况如下表:
则这10名同学年龄的平均数和中位数分别是13.5,13.5.
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数 | 1 | 4 | 4 | 1 |
 如图是一个有多个相同小正方体堆积而成的几何体,该几何体的左视图是( )
如图是一个有多个相同小正方体堆积而成的几何体,该几何体的左视图是( )


