题目内容
19.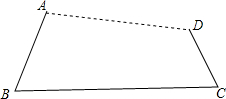 如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来
如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来(1)设橡皮筋AD的长是x(cm),若AB=5cm,CD=3cm,BC=11cm,求x的最大值和最小值;
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?
分析 (1)最大值应该是所有其他三条线段的和,最小值是用最大的线段的长减去其他两条相对较短的线段的长;
(2)根据(1)中的最大值和最小值即可确定x的取值范围.
解答 解:1.最大是5+3+11=19 最小是11-3-5=3;
2.由(1)得橡皮筋长x的取值范围为:3<x<19.
点评 本题考查了三角形的三边关系,解题的关键是了解x什么时候能取到最大值,什么时候能取到最小值,难度不大.

练习册系列答案
相关题目
8.下列运算中,错误的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | $\sqrt{1{6}^{2}+{9}^{2}}$=16+9=25 | ||
| C. | 2$\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
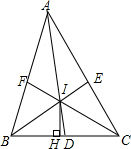 如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC.
如图,在△ABC中,三角形内角平分线AD,BE,CF相交于点I,IH⊥BC于点H,求证:∠BID=∠HIC. 已知:如图,甲、乙两人分别从正方形广场ABCD的顶点B、C同时出发,甲由点C向点D运动,乙向点B向点C运动,甲的速度为1km/h,乙的速度为2km/h,若正方形广场的周长为4km,问多长时间后,两人相距$\sqrt{2}$km?
已知:如图,甲、乙两人分别从正方形广场ABCD的顶点B、C同时出发,甲由点C向点D运动,乙向点B向点C运动,甲的速度为1km/h,乙的速度为2km/h,若正方形广场的周长为4km,问多长时间后,两人相距$\sqrt{2}$km?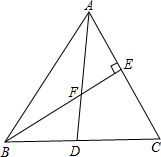 如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.
如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.