题目内容
9.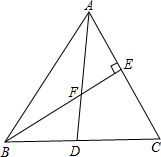 如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.
如图,锐角△ABC中.AD是∠BAC的平分线.线段BE垂直AC于E点.交线段AD于F.(1)试判断∠ABC和∠C、∠BFD之间存在何种等量关系,请证明:
(2)如果∠BAC是钝角,其他条件不变,(1)中结论是否成立?如不成立.又有怎样相应的结论?请画图证明.
分析 (1)如图1,由AD是∠BAC的平分线,得到∠1=∠2=$\frac{1}{2}∠$BAC=$\frac{1}{2}$(180°-∠ABC-∠ACB)=90°-$\frac{1}{2}$(∠ABC+∠C),由于BE⊥AC,得到∠2+∠ADE=90°,根据对顶角的性质得到∠2=90°-∠BFD,于是得出结论;
(2)如图2,由AD是∠BAC的平分线,得到∠1=∠2=$\frac{1}{2}∠$BAC=$\frac{1}{2}$(180°-∠ABC-∠ACB)=90°-$\frac{1}{2}$(∠ABC+∠C),根据BE⊥AC,得到∠EAF+∠BFD=90°,由对顶角相等得到∠2=∠EAF,于是得到结论.
解答 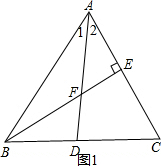 解:(1)如图1,∵AD是∠BAC的平分线,
解:(1)如图1,∵AD是∠BAC的平分线,
∴∠1=∠2=$\frac{1}{2}∠$BAC=$\frac{1}{2}$(180°-∠ABC-∠ACB)=90°-$\frac{1}{2}$(∠ABC+∠C),
∵BE⊥AC,
∴∠2+∠ADE=90°,
∵∠AFE=∠DFB,
∴∠2=90°-∠BFD,
∴∠BFD=$\frac{1}{2}$(∠ABC+∠C);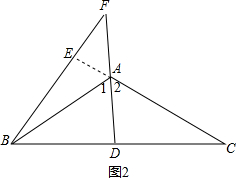
(2)(1)中结论成立,
如图2,∵AD是∠BAC的平分线,
∴∠1=∠2=$\frac{1}{2}∠$BAC=$\frac{1}{2}$(180°-∠ABC-∠ACB)=90°-$\frac{1}{2}$(∠ABC+∠C),
∵BE⊥AC,
∴∠EAF+∠BFD=90°,
∵∠2=∠EAF,
∴∠2+∠BFD=90°,
∴∠2=90°-∠BFD,
∴∠BFD=$\frac{1}{2}$(∠ABC+∠C).
点评 本题考查了三角形的内角和,角平分线的定义,对顶角的性质,正确的作出图形是解答(2)问的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
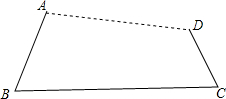 如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来
如图,用钉子把木棒AB、BC和CD分别在端点B、C处连接起来,用橡皮筋把AD连接起来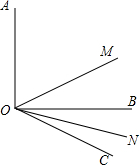 (1)如图所示,OM平分∠AOC,ON平分∠BOA
(1)如图所示,OM平分∠AOC,ON平分∠BOA 如图,在?ABCD中对角线AC,BD相交于点O,∠1=∠2,试判断四边形ABCD的形状,并证明你的结论.
如图,在?ABCD中对角线AC,BD相交于点O,∠1=∠2,试判断四边形ABCD的形状,并证明你的结论. 如图,圆锥的高为4cm,底面直径为6cm,现有一只蚂蚁在圆锥的顶部A处,它想吃到底部B处的食物,需爬行的最短路线是多少?
如图,圆锥的高为4cm,底面直径为6cm,现有一只蚂蚁在圆锥的顶部A处,它想吃到底部B处的食物,需爬行的最短路线是多少?