题目内容
2.我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.(1)若函数有两个不重合的零点时,求k的取值范围;
(2)若函数的两个零点都是整数点,求整数k的值;
(3)当k<0时,在(2)的条件下,函数的两个零点分别是点A,B(点A在点B的左侧),将二次函数的图象在点A,B间的部分(含点A和点B)向左平移n(n>0)个单位后得到的图象记为G,同时将直线y=-4kx+3向上平移n个单位.请结合图象回答:当平移后的直线与图象G有公共点时,求n的取值范围.
分析 (1)直接求出△的值,进而得出k的取值范围;
(2)令y=0,直接解方程得出符合题意的k的值;
(3)首先求出A,B点坐标,进而表示出A′,B′点坐标,再表示出平移后解析式,进而得出n的取值范围.
解答 (1)证明:△=(4k+1)2-4k(3k+3)=(2k-1)2,
∵二次函数有两个不重合的零点,
∴2k-1≠0,即k≠$\frac{1}{2}$,
∵k≠0,
∴当k≠0且k≠$\frac{1}{2}$时,二次函数有两个不重合的零点;
(2)解:当y=0,则0=kx2-(4k+1)x+3k+3,
解方程得:x=$\frac{(4k+1)±\sqrt{(2k-1)^{2}}}{2k}$,
∴x=3或x=1+$\frac{1}{k}$,
∵函数的两个零点都是整数,k是整数,
∴$\frac{1}{k}$是整数.
∴k=±1;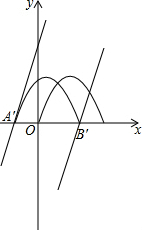
(3)解:∵k<0,
∴k=-1.
∴y=-x2+3x,y=4x+3.
∵函数的两个零点分别是A,B(点A在点B的左侧),
∴A(0,0),B(3,0).
∴平移后的点为:A′(-n,0),B′(3-n,0).
平移后的解析式为:y=4x+3+n.
∴-4n+3+n=0,
解得:n=1,
4(3-n)+3+n=0,
解得:n=5,
∴1≤n≤5.
点评 本题考查了二次函数和一次函数的性质,平移的性质,根的判别式等知识点的应用,通过做此题培养了学生的分析问题和解决问题的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
4.若|a-1|+|b-2|=0,那么2ab=( )
| A. | -4 | B. | +4 | C. | -8 | D. | +8 |
11.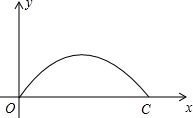 如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )
如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )
 如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )
如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )| A. | 18秒 | B. | 36秒 | C. | 38秒 | D. | 46秒 |
12.一年三班女生的人数是男生的$\frac{5}{6}$,如果男生有30人,那么一年三班共有( )
| A. | 25人 | B. | 5人 | C. | 55人 | D. | 50人 |
 已知:如图,△ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF,求证:∠EBO=∠FDO.
已知:如图,△ABCD的对角线AC,BD相交于点O,点E,F分别在AO,CO上,且AE=CF,求证:∠EBO=∠FDO. 如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).
如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).