题目内容
18.有五张正面分别标有数字-3,0,1,3,5的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,那么使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数的概率为$\frac{2}{5}$.分析 由使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数,可得x=$\frac{2}{2-a}$,即可得2-a>0且$\frac{2}{2-a}$≠2,继而求得使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数的a的值有:-3,0,再利用概率公式即可求得答案.
解答 解:方程两边同乘以x-2,得:1-ax+2(x-2)=-1,
解得:x=$\frac{2}{2-a}$,
∵使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数,
∴2-a>0且$\frac{2}{2-a}$≠2,
解得:a<2且a≠1,
∴使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数的a的值有:-3,0,
∴使得关于x的分式方程$\frac{1-ax}{x-2}+2=\frac{1}{2-x}$的解为正数的概率为:$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 此题考查了概率公式的应用以及分式方程的解的情况.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若$\sqrt{x-2}+\sqrt{1-y}$=0,则x-y的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
10.做任意抛掷一只纸杯的重复试验,记录杯口朝上的次数,获得如下数据:
估计任意抛掷一只纸杯,杯口朝上的概率是0.22.
| 抛掷总次数 | 100 | 150 | 200 | 300 |
| 杯口朝上的频数 | 21 | 32 | 44 | 66 |
8.下列变形,运用运算律正确的是( )
| A. | 2+(-1)=1+2 | B. | 3+(-2)+5=(-2)+3+5 | ||
| C. | [6+(-3)]+5=[6+(-5)]+3 | D. | $\frac{1}{3}$+(-2)+(+$\frac{2}{3}$)=($\frac{1}{3}$+$\frac{2}{3}$)+(+2) |
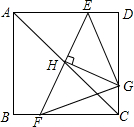 如图,经过正方形ABCD的对角线AC的中点H作直线和两边交于点E,F,再过点H作EF的垂线交边CD于点G,连接EG,FG
如图,经过正方形ABCD的对角线AC的中点H作直线和两边交于点E,F,再过点H作EF的垂线交边CD于点G,连接EG,FG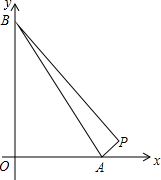 由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢?
由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢?