Question

7．如图①，△ABC中，BD平分∠ABC，且与△ABC的外角∠ACE的角平分线交于点D．
（1）若∠ABC=75°，∠ACB=45°，求∠D的度数；
（2）若把∠A截去，得到四边形MNCB，如图②，猜想∠D、∠M、∠N的关系，并说明理由．

Answer 1

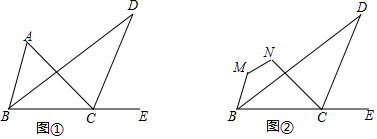
分析 （1）根据三角形内角和定理以及角平分线性质，先求出∠D、∠A的等式，推出∠A=2∠D，最后代入求出即可；
（2）根据（1）中的结论即可得到结论．

解答 解：∵∠ACE=∠A+∠ABC，
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE，∠DCE=∠D+∠DBC，
又BD平分∠ABC，CD平分∠ACE，
∴∠ABD=∠DBE，∠ACD=∠ECD，
∴∠A=2（∠DCE-∠DBC），∠D=∠DCE-∠DBC，
∴∠A=2∠D，
∵∠ABC=75°，∠ACB=45°，
∴∠A=60°，
∴∠D=30°；

（2）∠D=$\frac{1}{2}$（∠M+∠N-180°）；
理由：延长BM、CN交于点A，
则∠A=∠BMN+∠CNM-180°，
由（1）知，∠D=$\frac{1}{2}∠$A，
∴∠D=$\frac{1}{2}$（∠M+∠N-180°）．

点评 此题考查三角形内角和定理以及角平分线性质的综合运用，解此题的关键是求出∠A=2∠D．