Question

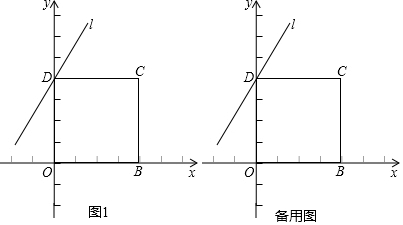
12．如图所示，在平面直角坐标系xOy中，B，C两点的坐标分别为B（4，0），C（4，4），CD⊥y轴于点D，直线l经过点D．
（1）直接写出点D的坐标；
（2）作CE⊥直线l于点E，将直线CE绕点C逆时针旋转45°，交直线l于点F，连接BF．
①依题意补全图形；
②通过观察、测量，同学们得到了关于直线BF与直线l的位置关系的猜想，请写出你的猜想；
③通过思考、讨论，同学们形成了证明该猜想的几种思路：
思路1：作CM⊥CF，交直线l于点M，可证△CBF≌△CDM，进而可以得出∠CFB=45°，从而证明结论．
思路2：作BN⊥CE，交直线CE于点N，可证△BCN≌△CDE，进而证明四边形BFEN为矩形，从而证明结论．
…
请你参考上面的思路完成证明过程．（一种方法即可）
解：（1）点D的坐标为（0，4），
（2）①补全图形，
②直线BF与直线l的位置关系是BF⊥直线l，
③证明：

Answer 1

分析 （1）由C（4，4），CD⊥y轴于D，即可推出D（0，4）；
（2）①画出图形即可．
②结论：BF⊥直线l．
③证法一：如图2中，作CM⊥CF交直线l于M．想办法证明△CBF≌△CDM即可解决问题；
证法二：如图3中，作BN⊥CE于N．只要证明四边形EFBN是矩形即可；

解答 解：（1）∵C（4，4），CD⊥y轴于D．
∴D（0，4）．
故答案为（0，4）．

（2）①补全的图形如图1所示，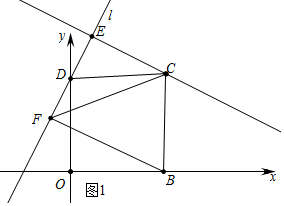

②结论：BF⊥直线l．
③证明：方法一：如图2中，作CM⊥CF交直线l于M．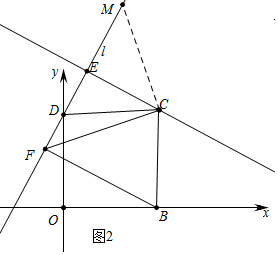

∵B（4，0），C（4，4），D（0，4），
∴OB=BC=DC=OD=4，∠BCD=90°，
∵CE⊥直线l，CM⊥CF，∠ECF=45°，
∴△CEF，△CEM都是等腰直角三角形，
∴∠CMD=∠CFE=45°，
∴CF=CM，
∵○FCM=○DCB，
∴∠DCM=∠FCB，∴CD=BC，
∴△CBF≌△CDM，
∴∠CFB=∠CMD=45°，
∴∠BFE=∠CFB+∠CFE=90°，
∴BF⊥直线l．

方法二：如图3中，作BN⊥CE于N．

∵∠CED=∠BNC=90°，
∴∠1+∠3=90°，∠2+∠3=90°，
∴∠1=∠2，∵BC=CD，
∴△BCN≌△CDE，
∴BN=CE，
∵EF=EC，
∴EF=BN，∵BN∥EF，
∴四边形EFBN是平行四边形，
∵∠FEN=90°，
∴四边形EFBN是矩形，
∴∠EFB=90°，
∴NF⊥直线l．
故答案为BF⊥直线l．

点评 本题考查四边形综合题．正方形的判定和性质、矩形的判定和性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考压轴题．