题目内容
19.(1)计算:-($\frac{1}{4}$)-1+(-2)2×(-2017)0(2)解不等式组:$\left\{\begin{array}{l}{x-6>-2x}\\{\frac{1}{2}x<3}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)根据负整数指数幂、零指数幂、有理数的乘方分别求出每一部分的值,再带求出即可;
(2)先求出每个不等式的解集,再求出不等式组的解集,最后表示出来即可.
解答 解:(1)原式=-4+4×1
=0;
(2)$\left\{\begin{array}{l}{x-6>-2x①}\\{\frac{1}{2}x<3②}\end{array}\right.$
∵解不等式①得:x>2,
解不等式②得:x<6,
∴不等式组的解集为2<x<6,
在数轴上表示为: .
.
点评 本题考查了负整数指数幂、零指数幂、有理数的乘方,解一元一次不等式组,在数轴上表示不等式组的解集等知识点,能灵活运用运用知识点求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{1-2x>x-2}\end{array}\right.$的解集中只有4个整数解,则a取值范围是-4≤a<-3.
8.下列计算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | $\sqrt{12}$=2$\sqrt{3}$ |
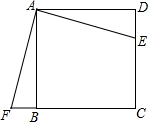 如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形.
如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形.