题目内容
14. 如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.
如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.
分析 作点B关于AC的对称点F,构建直角三角形,根据最短路径可知:此时PB+PE的值最小,接下来要求出这个最小值,即求EF的长即可,因此要先求AF的长,证明△ADF≌△CDB,可以解决这个问题,从而得出EF=5,则PB+PE的最小值为5.
解答  解:如图,过B作BD⊥AC,垂足为D,并截取DF=BD,连接EF交AC于P,连接PB、AF,则此时PB+PE的值最小,
解:如图,过B作BD⊥AC,垂足为D,并截取DF=BD,连接EF交AC于P,连接PB、AF,则此时PB+PE的值最小,
∵△ABC是等腰直角三角形,
∴AB=CB,∠ABC=90°,AD=DC,
∴∠BAC=∠C=45°,
∵∠ADF=∠CDB,
∴△ADF≌△CDB,
∴AF=BC,∠FAD=∠C=45°,
∵AE=3,BE=1,
∴AB=BC=4,
∴AF=4,
∵∠BAF=∠BAC+∠FAD=45°+45°=90°,
∴由勾股定理得:EF=$\sqrt{A{F}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵AC是BF的垂直平分线,
∴BP=PF,
∴PB+PE=PF+PE=EF=5,
故答案为:5.
点评 本题考查了等腰直角三角形和轴对称的最短路径问题,要先找到符合条件的点P,可以通过轴对称来确定,即作出其中一点关于直线AC的对称点,对称点与另一点的连线与AC的交点就是所要找的点.再构造直角三角形利用勾股定理解决.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.下列说法正确的是( )
| A. | 两个矩形一定相似 | B. | 两个菱形一定相似 | ||
| C. | 两个等腰三角形一定相似 | D. | 两个等边三角形一定相似 |
8.如果|-3x|=3x,则x的取值范围是( )
| A. | x>0 | B. | x≥0 | C. | x≤0 | D. | x<0 |
4. 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( )
如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( )
 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( )
如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( )| A. | 25个单位长度 | B. | 14个单位长度 | C. | 12个单位长度 | D. | 10个单位长度 |
10.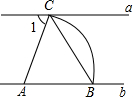 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )| A. | 36° | B. | 54° | C. | 72° | D. | 63° |
4.一元二次方程3x2-4=-2x的二次项系数、一次项系数、常数项分别为( )
| A. | 3,-4,-2 | B. | 3,-2,-4 | C. | 3,2,-4 | D. | 3,-4,0 |
 已知a,b,c满足(c-5)2+|a+b|=0,且b是最小的正整数,数轴上A,B,C各点所对应的数分别为a,b,c,解答下列问题:
已知a,b,c满足(c-5)2+|a+b|=0,且b是最小的正整数,数轴上A,B,C各点所对应的数分别为a,b,c,解答下列问题: