题目内容
10.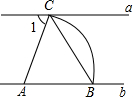 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )| A. | 36° | B. | 54° | C. | 72° | D. | 63° |
分析 根据等腰三角形性质求出∠ACB,根据三角形的内角和定理求出∠CAB,根据平行线性质求出即可.
解答 解:∵AC=AB,
∴∠ACB=∠ABC=54°,
∵根据三角形的内角和定理得:∠ACB+∠ABC+∠CAB=180°,
∴∠CAB=180°-∠ACB-∠ABC=180°-54°-54°=72°,
∵l1∥l2,
∴∠1=∠CAB=72°,
故选C.
点评 本题考查了对等腰三角形的性质,三角形的内角和定理,平行线的性质等知识点的理解和掌握,关键是求出∠CAB的度数,主要考查学生运用定理进行推理的能力,题型较好.

练习册系列答案
相关题目
3.如果+160元表示增加160元,那么-60元表示( )
| A. | 增加100元 | B. | 增加60元 | C. | 减少60元 | D. | 减少220元 |
1.下面的图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列运算正确的是( )
| A. | -a(a-b)=-a2-ab | B. | (2ab)2+a2b=4ab | C. | 2ab?3a=6a2b | D. | (a-1)(1-a)=a2-1 |
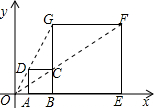 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2). ________________.
________________. 如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.
如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.