题目内容
3. 已知a,b,c满足(c-5)2+|a+b|=0,且b是最小的正整数,数轴上A,B,C各点所对应的数分别为a,b,c,解答下列问题:
已知a,b,c满足(c-5)2+|a+b|=0,且b是最小的正整数,数轴上A,B,C各点所对应的数分别为a,b,c,解答下列问题:(1)填空:a=-1,b=1,c=5.
(2)点M在点A左侧,其对应的数为x,化简|2x|(要求说明埋由).
(3)点P从点A出发以每秒1个单位长度的速度向左运动,点Q从点B出发以每秒2个单位长度的速度向右运动,点R从点C出发以每秒5个单位长度的速度向右运动,这三个点同时出发,设运动时间为t秒,若点P与点Q之间的距离表示为m,点Q与点R之间的距离表示为n,问:n-m的值与1的值是否有关?
分析 (1)根据非负数的性质求得a、b、c的值;
(2)点M在点A左侧,则x<0,由此化简|2x|;
(3)分别用t表示出动点P、Q、R所表示的数,然后求得m-n的值,则易得n-m的值与1的值是否有关.
解答 解:(1)∵b是最小的正整数,
∴b=1,
∵(c-5)2+|a+b|=0,
∴c-5=0,a+b=0,
∴c=5,b=1,a=-1,
故答案是:-1;1;5;
(2)由(1)知,a=-1,a在数轴上所对应的点分别为A,
∵点M在点A左侧,
∴x<0,
∴|2x|=-2x;
(3)t秒时,点P表示的数为:-1-t,
点Q表示的数为:1+2t,
点R表示的数为:5+5t,
则m=PQ=1+2t-(-1-t)=3t+2,
n=QR=5+5t-1-2t=3t+4,
∴n-m=3t+4-3t-2=2,
则n-m的值与1没有关系,n-m=2.
点评 本题考查了数轴与绝对值,通过数轴把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
16.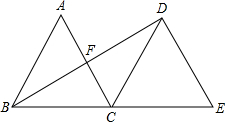 如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( )
如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( )
 如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( )
如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 2$\sqrt{3}$ |
11.下列等式从左到右的变形中,属于因式分解的是( )
| A. | x2-9=(x+3)(x-3) | B. | x2+5x-1=x(x+5)-1 | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | (x+2)(x-2)=x2-4 |
11.多项式4x2+1加上一个一次单项式后是一个完全平方式,这个单项式应为( )
| A. | 4x | B. | -4x | C. | ±2x | D. | ±4x |
 如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.
如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为5.
 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )