题目内容
5.在5×5的网格中有线段AB,在网格线的交点上找一点C,使三角形ABC满足如下条件.(仅用直尺作图)(1)在网格①中作一个等腰三角形ABC;
(2)在网格②中作一个直角三角形ABC,使两直角边的长为无理数.
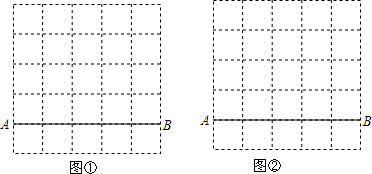
分析 (1)由勾股定理得出$\sqrt{{3}^{2}+{4}^{2}}$=5=AB,作AC=5,或BC=5,画出图形即可;
(2)由勾股定理得出12+22=5,22+42=20,5+20=25=AB2,由勾股定理的逆定理得出直角三角形,画出图形即可.
解答 解:(1)∵$\sqrt{{3}^{2}+{4}^{2}}$=5,AB=5,
∴作AC=5,或BC=5,
△ABC如图1所示:
(2)∵$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
($\sqrt{5}$)2+(2$\sqrt{5}$)2=5+20=25=AB2,
∴画出△ABC和△ABC1是直角三角形,
如图2所示.
点评 本题考查了勾股定理、勾股定理的逆定理、等腰三角形的判定;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算与作图是解题的关键.

练习册系列答案
相关题目
10.下列各题中计算正确的是( )
| A. | 3x2-x2=2 | B. | (a3)2•a5=a30 | C. | (x2)3•x+x5•x2=2x7 | D. | (-a2)3=a6 |

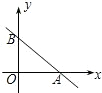 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.