Question

10．△ABC中，D、E分别在AB、AC上，AD=4，DB=2，AC=8，当AE=$\frac{16}{3}$时，△ADE∽△ABC；当AE=3时，△ADE∽△ACB．

Answer 1

分析 根据两组对应边的比相等且夹角对应相等的两个三角形相似可得当$\frac{AD}{AB}$=$\frac{AE}{AC}$时，△ADE∽△ABC，当$\frac{AE}{AB}$=$\frac{AD}{AC}$时，△ADE∽△ACB，然后再代入数值进行计算即可．

解答 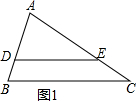解：如图1：当AE=$\frac{16}{3}$时，△ADE∽△ABC，
∵AD=4，DB=2，
∴AB=6，
∵当$\frac{AD}{AB}$=$\frac{AE}{AC}$时，△ADE∽△ABC，
∴$\frac{4}{4+2}$=$\frac{AE}{8}$，
解得：AE=$\frac{16}{3}$；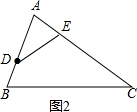
如图2，当AE=3时，△ADE∽△ACB．
当$\frac{AE}{AB}$=$\frac{AD}{AC}$时，△ADE∽△ACB，
∵AD=4，DB=2，AC=8，
∴$\frac{AE}{6}$=$\frac{4}{8}$，
解得：AE=3，
故答案为：$\frac{16}{3}$；3．

点评 此题主要考查了相似三角形的判定，关键是掌握两组对应边的比相等且夹角对应相等的两个三角形相似．