题目内容
1. 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米.
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为2a米,宽为b米.(1)请用代数式表示广场空地的面积:(2ab-πr2)平方米;
(2)若a=200米,b=100米,圆形花坛的半径为15米,求广场空地的面积(π=3).
分析 (1)观察可得空地的面积=长方形的面积-圆的面积,把相关数值代入即可;
(2)把所给数值代入(1)得到的代数式求值即可.
解答 解:(1)空地的面积=2ab-πr2(平方米);
(2)当a=200,b=100,r=15时,
空地的面积=2×200×100-3×152=40000-675=3325(平方米).
答:广场空地的面积是3325平方米.
故答案为:(2ab-πr2).
点评 此题主要考查了列代数式及代数式的相关计算;得到空地部分的面积的关系式是解决本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12.下列从左到右的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x=x(x+2) | C. | m2+m-4=m(m+1)-4 | D. | 2x2+2x=2x2(1+$\frac{1}{x}$) |
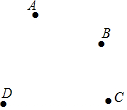 如图所示,平面上有四个点A、B、C、D,根据下列语句画图:
如图所示,平面上有四个点A、B、C、D,根据下列语句画图: