题目内容
 如图,点D在以AC为直径的⊙O上,若∠BDC=35°,那么∠ACB的度数是( )
如图,点D在以AC为直径的⊙O上,若∠BDC=35°,那么∠ACB的度数是( )| A、35° | B、55° |
| C、70° | D、110° |
考点:圆周角定理
专题:
分析:由AC为⊙O的直径,根据直径所对的圆周角是直角,即可求得∠ABC的度数,然后由圆周角定理,求得∠A的度数,继而求得答案.
解答:
解:∵AC为⊙O的直径,
∴∠ABAC=90°,
∵∠A=∠BDC=35°,
∴∠ACB=90°-∠A=55°.
故选B.
∴∠ABAC=90°,
∵∠A=∠BDC=35°,
∴∠ACB=90°-∠A=55°.
故选B.
点评:此题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
| A、10m | B、3m |
| C、4m | D、2m或10m |
在直角坐标系中,一直线l向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-
,0),则直线l的函数关系式为( )
| 3 |
A、y=-
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
如图1,圆的周长为4个单位.在该圆的4等分点处分别标上字母m、n、p、q.如图2,先将圆周上表示p的点与数轴原点重合,然后将该圆沿着数轴的负方向滚动,则数轴上表示-2013的点与圆周上重合的点对应的字母是( )


| A、m | B、n | C、p | D、q |
两个多边形相似的条件是( )
| A、对应角相等 |
| B、对应边成比例 |
| C、对应角相等或对应边成比例 |
| D、对应角相等且对应边成比例 |


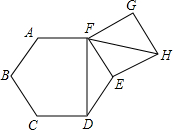 如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为
如图,在正六边形ABCDEF的外侧,作正方形EFGH,则∠DFH的度数为