题目内容
19．求不等式组$\left\{\begin{array}{l}7（x-1）＜4x+3\\ 6（\frac{2}{3}x+1）≥2x+1\end{array}\right.$的整数解．分析 先求出每个不等式的解集，再求出不等式组的解集，最后求出整数解即可．
解答 解：$\left\{\begin{array}{l}{7（x-1）＜4x+3①}\\{6（\frac{2}{3}x+1）≥2x+1②}\end{array}\right.$
∵由①得 7x-7＜4x+3，
3x＜10，
$x＜\frac{10}{3}$，
由②得 4x+6≥2x+1，
2x≥-5，
$x≥-\frac{5}{2}$，
∴不等式组的解集为：$-\frac{5}{2}≤x＜\frac{10}{3}$，
它的整数解为-2，-1，0，1，2，3．
点评 本题考查了解一元一次不等式组，不等式组的整数解的应用，解此题的关键是能求出不等式组的解集，难度适中．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
10．如果a＞b，那么下列不等式一定成立的是（ ）
| A． | a-b＜0 | B． | -a＞-b | C． | $\frac{1}{2}$a＜$\frac{1}{2}$b | D． | 2a＞2b |
7．某公司三月份的产值为a万元，比二月份增长了m%，那么二月份的产值（单位：万元）为（ ）
| A． | a（1+m%） | B． | a（1-m%） | C． | $\frac{a}{1+m%}$ | D． | $\frac{a}{1-m%}$ |
4．不等式组$\left\{\begin{array}{l}{2x+1≥0}\\{x-1＜0}\end{array}\right.$的解集是（ ）
| A． | x≥-$\frac{1}{2}$ | B． | x＜1 | C． | -$\frac{1}{2}$≤x＜1 | D． | -$\frac{1}{2}$＜x＜1 |
8．
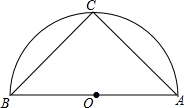如图，在以AB为直径的半圆O中，点C是$\widehat{AB}$的中点，若AC=4，则△ABC的面积是（ ）
如图，在以AB为直径的半圆O中，点C是$\widehat{AB}$的中点，若AC=4，则△ABC的面积是（ ）| A． | 3.5 | B． | 8 | C． | 12 | D． | 16 |