题目内容
11.解方程组:$\left\{\begin{array}{l}{{x}^{2}+6xy+9{y}^{2}=1}\\{x-y-3=0}\end{array}\right.$.分析 把①化为x+3y=1和x+3y=-1,再把x+3y=1和x+3y=-1分别与x-y-3=0组成方程组,解出方程组得到答案.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+6xy+9{y}^{2}=1①}\\{x-y-3=0②}\end{array}\right.$,
由①得,(x+3y)2=1
即x+3y=1,x+3y=-1,
得到方程组$\left\{\begin{array}{l}{x+3y=1}\\{x-y-3=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+3y=-1}\\{x-y-3=0}\end{array}\right.$,
分别解这两个方程组,得原方程组的解:$\left\{\begin{array}{l}{{x}_{1}=2\frac{1}{2}}\\{{y}_{1}=-\frac{1}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=-1}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,把二元二次方程通过因式分解化为两个二元一次方程,再把这两个二元一次方程分别与另一个方程组成二元一次方程组,解方程组即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.关于x的方程2x2-3x-1=0的解的情况,正确的是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
6.下列命题中,真命题是( )
| A. | 有两边和一角对应相等的两个三角形全等 | |
| B. | 有两边和第三边上的高对应相等的两个三角形全等 | |
| C. | 有两边和其中一边上的高对应相等的两个三角形全等 | |
| D. | 有两边和第三边上的中线对应相等的两个三角形全等 |
16.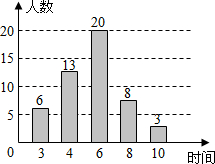 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
 为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
1.顺次连接菱形ABCD各边中点所得到的四边形一定是( )
| A. | 菱形 | B. | 正方形 | ||
| C. | 矩形 | D. | 对角线互相垂直的四边形 |