题目内容
?ABCD的对角线AC,BD交于点O,若△AOB的面积为5,则?ABCD的面积为( )
| A、10 | B、15 | C、20 | D、25 |
考点:平行四边形的性质
专题:
分析:因为平行四边形的对角线互相平分,所以平行四边形被对角线分成的四部分的面积相等,即?ABCD的面积=△AOB的面积×4.
解答: 解:∵点O是平行四边形ABCD的对角线AC和BD的交点,
解:∵点O是平行四边形ABCD的对角线AC和BD的交点,
∴OA=OC,OB=OD,
在△AOB与△COD中,
,
∴△AOB≌△COD(SAS).
同理,△BOC≌△DOA.
又∵AO是△ABD的中线,
∴△AOB与△AOD的面积相等,
故?ABCD的面积=△AOB的面积×5=4×5=20.
故选:C.
 解:∵点O是平行四边形ABCD的对角线AC和BD的交点,
解:∵点O是平行四边形ABCD的对角线AC和BD的交点,∴OA=OC,OB=OD,
在△AOB与△COD中,
|
∴△AOB≌△COD(SAS).
同理,△BOC≌△DOA.
又∵AO是△ABD的中线,
∴△AOB与△AOD的面积相等,
故?ABCD的面积=△AOB的面积×5=4×5=20.
故选:C.
点评:本题考查了平行四边形的性质.解题时,充分利用了平行四边形的对角线互相平分的性质.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
某校八年级有六个班,一次测试后,分别求得各个班级学生成绩的平均数,它们不完全相同,下列说法正确的是( )
| A、全年级学生的平均成绩一定在这六个平均成绩的最小值与最大值之间 |
| B、将六个平均成绩之和除以6,就得到全年级学生的平均成绩 |
| C、这六个平均成绩的最大值与最小值的一半就是全年级学生的平均成绩 |
| D、这六个平均成绩的最大值与最小值的一半不可能是全年级学生的平均成绩 |
下列说法中,正确的是( )
①cosα表示∠α与符号cos的乘积;
②在△ABC中,∠C=90°,则c=b•sinB;
③在直角三角形中,不论三角形的边长大小如何,如果其中一个锐角为20°不变,那么20°角的各三角函数值的大小也不变;
④在直角三角形中,锐角A的正弦值在0和1之间.
①cosα表示∠α与符号cos的乘积;
②在△ABC中,∠C=90°,则c=b•sinB;
③在直角三角形中,不论三角形的边长大小如何,如果其中一个锐角为20°不变,那么20°角的各三角函数值的大小也不变;
④在直角三角形中,锐角A的正弦值在0和1之间.
| A、①② | B、③④ | C、②③ | D、①④ |
若
=5-a,则a与5的大小关系为( )
| (a-5)2 |
| A、a<5 | B、a>5 |
| C、a≥5 | D、a≤5 |
方程
=
的解为( )
| 1 |
| 2x |
| 1 |
| x2+1 |
| A、1 | B、-1 | C、±1 | D、0 |
在平面直角坐标系中,两圆的圆心坐标分别为(-1,0)和(0,
),半径都是1,那么这两圆的位置关系是( )
| 3 |
| A、外离 | B、相切 | C、相交 | D、内含 |
小明在解方程x2-x=0时,只得出一个根是1,则被漏掉的一个根是( )
| A、x=0 | B、x=1 |
| C、x=2 | D、x=3 |
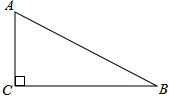 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )| A、相离 | B、相交 | C、相切 | D、不确定 |