题目内容
下列说法中，正确的是（ ）
①cosα表示∠α与符号cos的乘积；
②在△ABC中，∠C=90°，则c=b•sinB；
③在直角三角形中，不论三角形的边长大小如何，如果其中一个锐角为20°不变，那么20°角的各三角函数值的大小也不变；
④在直角三角形中，锐角A的正弦值在0和1之间．
①cosα表示∠α与符号cos的乘积；
②在△ABC中，∠C=90°，则c=b•sinB；
③在直角三角形中，不论三角形的边长大小如何，如果其中一个锐角为20°不变，那么20°角的各三角函数值的大小也不变；
④在直角三角形中，锐角A的正弦值在0和1之间．
| A、①② | B、③④ | C、②③ | D、①④ |
考点：锐角三角函数的定义,锐角三角函数的增减性
专题：
分析：根据三角函数的定义即可解答．
解答：解：①错误；
②在△ABC中，∠C=90°，sinB=
，则c=
，命题错误；
③正确；
④正确．
故选A．
②在△ABC中，∠C=90°，sinB=
| b |
| c |
| b |
| sinB |
③正确；
④正确．
故选A．
点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．三角函数的大小是由角的大小确定的，与所在三角形无关．
练习册系列答案
相关题目
如图，AB为⊙O的直径，AB=AC，AC交于⊙O点E，∠BAC=45°．若AE=1，则BC=下列各式计算正确的是（ ）
A、
| ||||||||||||
B、（2+
| ||||||||||||
C、（
| ||||||||||||
D、（-
|
四个小朋友在公园玩跷跷板，他们的体重分别为P，Q，R，S，由图可知，这四个小朋友体重的大小关系是（ ）| A、P＞R＞S＞Q |
| B、Q＞S＞P＞R |
| C、S＞P＞Q＞R |
| D、S＞P＞R＞Q |
如图，已知一商场自动扶梯的长l为10m，该自动扶梯到达的高度h为5m，自动扶梯与地面所成的角为θ，则tanθ的值等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平面直角坐标系中，半径均为
的两圆的圆心坐标分别是（0，0）和（0，2），则两圆的位置关系是（ ）
| 2 |
| A、内含 | B、相交 | C、外切 | D、外离 |
如图，AB是⊙O的直径，弦AC，BD相交于点P，则| CD |
| AB |
| A、sin∠BPC |
| B、cos∠BPC |
| C、tan∠BPC |
| D、以上都不对 |
?ABCD的对角线AC，BD交于点O，若△AOB的面积为5，则?ABCD的面积为（ ）
| A、10 | B、15 | C、20 | D、25 |
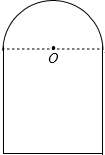如图所示为上边是半圆，下边是长方形的桥洞，已知半圆的直径为2.2米，长方形的另一边为2.3米，有一辆装满货物的卡车，高2.5米，宽1.6米，要从此桥洞经过．