Question

【题目】已知正方形的边长为4，点，分别在边，上，且，直线与直线交于点，直线交直线于点，连接，．

（1）如图1，当时，求证：平分；

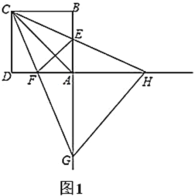
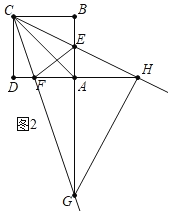
（2）如图2，将图1中的绕点逆时针旋转，其他条件不变，（1）的结论是否成立？说明理由；

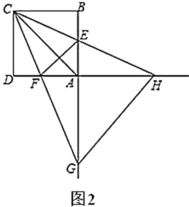
（3）当是等腰三角形时，直接写出的长．

Answer 1

【答案】（1）证明见解析；（2）成立，理由见解析；（3）AG的长为4或或8

【解析】

（1）先证CDF≌CBE，进而可得，CF＝CE，由此可得∠DFC＝67.5°，再根据，CF＝CE可求得，进而可证得FC平分∠DFE；

（2）延长AD到M，使DM＝BE，先证DMC≌BEC，可得CM＝CE，∠MCD＝∠ECB，再证MCF≌ECF，由此可得∠MFC＝∠EFC，进而可证得FC平分∠DFE；

（3）分三种情形画出图形分别求解即可解决问题．

（1）证明：∵四边形ABCD是正方形，

∴CD＝CA，∠B＝∠D＝∠DCA＝90°

又DF＝BE，

∴CDF≌CBE（SAS）

∴，CF＝CE，

∴∠DFC＝90°－22.5°＝67.5°，，

∴∠DFC＝∠CFE，

∴FC平分∠DFE；

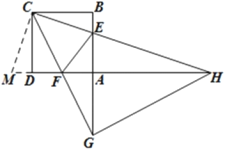
（2）解：成立，

延长AD到M，使DM＝BE，

∵四边形ABCD是正方形，

∴CB＝CD，∠CDA＝∠B＝∠DCB＝90°，

∴∠DCF+∠ECB＝90°－∠ECF＝45°，

∵∠CDM＝180°－∠CDA＝90°＝∠B

∴DMC≌BEC（SAS）

∴CM＝CE，∠MCD＝∠ECB，

∴∠DCF+∠MCD＝45°，

即∠MCE＝∠ECF＝45°，

又CF＝CF，

∴MCF≌ECF（SAS），

∴∠MFC＝∠EFC，

∴FC平分∠DFE，

（3）解：如图1，当GC＝GH时，

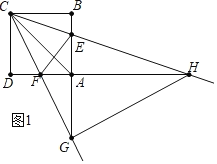
∵∠GCH＝45°，

∴∠GHC＝∠GCH＝45°，

∴∠CGH＝90°，

∴∠CGB+∠AGH＝90°，

∵∠B＝90°，

∴∠CGB+∠BCG＝90°，

∴∠AGH＝∠BCG，

∴AHG≌BGC（AAS），

∴AG＝BC＝4；

如图2，当CH＝HG时，

同理可以证明GAH≌HDC

∴AH＝BC＝4，

∴AG＝DH＝AD+AH＝8．

如图3，当CG＝CH时，

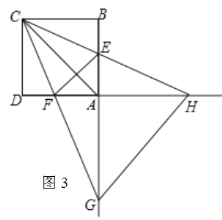
则∠CGH＝∠CHG＝(180°﹣45°)＝67.5°．

∵∠B＝∠D＝90°，CD＝CB，CH＝CG，

∴RtCDH≌RtCBG（HL）

∴DH＝BG，

又∵AD＝AB，

∴AH＝AG，

∴∠AGH＝∠AHG＝45°，

∴∠AGC＝∠CGH﹣∠AGH＝22.5°，

∵CG＝CH，AC＝AC，AG＝AH，

∴DMC≌BEC（SSS），

∴∠ACG＝∠ACH＝22.5°，

∴∠ACG＝∠AGC，

∴AC＝AG，

∵在RtACD中，AC＝，

∴AG＝，

综上所述，AG的长为4或或8．