Question

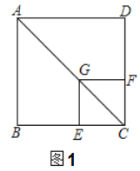
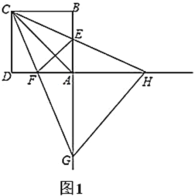
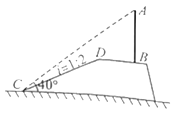
【题目】如图，两个大小不同的三角板放在同一平面内，直角顶点重合于点，点在上，，与交于点，若，，则_________．

Answer 1

【答案】

【解析】

过点C作CM⊥DE于点M，先证BCD∽ACE，求出AE的长及∠CAE＝60°，推出∠DAE＝90°，在RtDAE中利用勾股定理求出DE的长，进一步求出CE的长，再证AFD∽EFC，利用相似三角形对应边的比相等即可求出的比值．

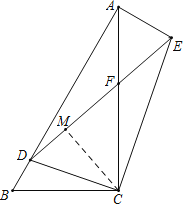
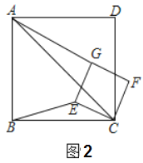
解：如图，过点C作CM⊥DE于点M，

∵BD＝2，AD＝8，

∴AB＝BD+AD＝10，

∵在Rt△ABC中，∠BAC＝30°，∠B＝90°﹣∠BAC＝60°，

∴BC＝AB＝5，AC＝BC＝5，

在RtBCA与RtDCE中，

∵∠BAC＝∠DEC＝30°，

∴tan∠BAC＝tan∠DEC，

∴，

∵∠BCA＝∠DCE＝90°，

∴∠BCA﹣∠DCA＝∠DCE﹣∠DCA，

∴∠BCD＝∠ACE，

∴BCD∽ACE，

∴∠CAE＝∠B＝60°，，

∴∠DAE＝∠DAC+∠CAE＝30°+60°＝90°，，

∴AE＝2，

在RtADE中，DE＝＝，

在RtDCE中，∠DEC＝30°，

∴∠EDC＝60°，CE＝DE＝，

∵∠BAC＝∠CEF，∠AFD＝∠EFC，

∴AFD∽EFC，

∴，

故答案为：．