题目内容
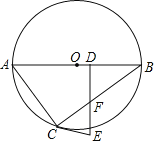
【题目】如图，
是
的直径，点
在上，点
为弦
的中点，射线
与圆周及切线
分别交于点
和点
，连接
．
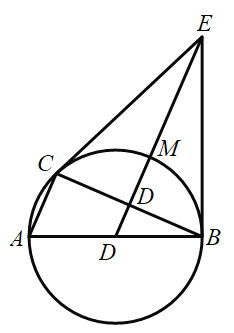
（1）求证：直线是的切线；
（2）若直径
，填空：①连接
，当
_________
时，四边形
是菱形；
②当
________时，四边形
是正方形．
【答案】（1）见解析；（2）①30；②
【解析】
（1）连接
，利用切线的性质与垂直平分线的性质证明
，即可得到结论；
（2）①利用菱形的性质证明
是等边三角形，结合直径所对的圆周角是直角可得结论，②利用正方形的性质求解
，即可得到答案．
（1）解：连接，
为
的切线，
，
点
为
的中点，
依据垂径定理得垂直平分，
在
和
中，
,
，
为半径，
直线
是的切线；
（2）①
；②
理由如下：①四边形
为菱形，
为等边三角形，
为的直径，
；
②四边形
为正方形，
，
；
故答案为①；②
练习册系列答案
相关题目
