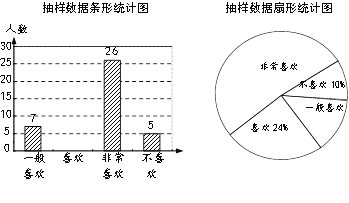
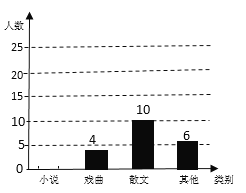
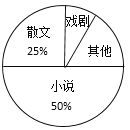
题目内容
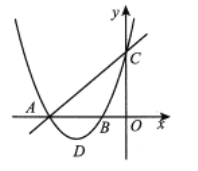
【题目】在平面直角坐标系xOy中,抛物线G:![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数
与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数![]() (
(![]() )的图像为直线
)的图像为直线![]() .
.
(1)求A、B两点的坐标;
(2)当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]() ,试说明:抛物线G的顶点不在直线
,试说明:抛物线G的顶点不在直线![]() 上;
上;
(3)设![]() ,直线
,直线![]() 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线
与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线![]() 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
【答案】(1)点A的坐标(-1,0),点B的坐标(3,0);(2)见解析;(3)4, 5,6,7,8
【解析】
(1)令![]() ,可解得A,B坐标;
,可解得A,B坐标;
(2)将![]() 配方为顶点式,得顶点坐标;确定1≤x≤2与对称轴的关系,表示出m,n的值;将顶点代入
配方为顶点式,得顶点坐标;确定1≤x≤2与对称轴的关系,表示出m,n的值;将顶点代入![]() 进行判断即可;
进行判断即可;
(3)当A、C两点到直线![]() 距离相等时,
距离相等时,![]() 过AC中点,确定直线
过AC中点,确定直线![]() ,表示点F坐标,确定点E坐标,求出BE所在直线的解析式,若F在BE上方,得不等式即可,求出n的取值范围,可得整数n.
,表示点F坐标,确定点E坐标,求出BE所在直线的解析式,若F在BE上方,得不等式即可,求出n的取值范围,可得整数n.
(1)令![]() ,得
,得![]() ,
,
即![]() ,解得
,解得![]()
∵A在B的左侧,
∴A(![]() ),B(3,0)
),B(3,0)
(2)由![]()
得顶点坐标为:(![]() ),对称轴为
),对称轴为![]()
∵![]() ,开口向下
,开口向下
∴当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]()
得![]() ,即
,即![]()
∴![]()
当![]() 时,
时,![]()
∴抛物线G的顶点不在直线![]() 上
上
(3)当![]() 时,
时,![]()
∴C(0,9)
∵A、C两点到直线![]() 距离相等
距离相等
∴直线![]() 过A,C两点的中点
过A,C两点的中点
∵A(![]() )
)
∴D(![]() )
)
将点D代入![]() 得:
得:![]() ,即
,即![]()
∴直线![]() 可化为:
可化为:![]()
∴E(0,![]() )
)
设BE的解析式为:![]()
则![]() ,解得
,解得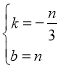
故BE的解析式为:![]()
∵点F为直线![]() 与对称轴交点
与对称轴交点
∴F(![]() )
)
又点F在直线BE上方
∴![]() ,解得
,解得![]()
又∵![]()
∴![]()
∵![]() 为整数
为整数
∴![]() .
.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目