题目内容
 如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于
如图,把一个长方形的纸片沿EF折叠后,点D、C分别落在点M、N的位置,如果∠EFB=65°,那么∠AEM等于考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:根据两直线平行,内错角相等可得∠DEF=∠EFB,再根据翻折的性质和平角等于180°列式计算即可得解.
解答:解:∵矩形对边AD∥BC,
∴∠DEF=∠EFB=65°,
∵沿EF折叠后,点D、C分别落在点M、N的位置,
∴∠DEF=∠MEF,
∴∠AEM=180°-65°×2=50°.
故答案为:50°.
∴∠DEF=∠EFB=65°,
∵沿EF折叠后,点D、C分别落在点M、N的位置,
∴∠DEF=∠MEF,
∴∠AEM=180°-65°×2=50°.
故答案为:50°.
点评:本题考查了平行线的性质,翻折变换的性质,熟记各性质是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
下列各组中的两项,不是同类项的是( )
| A、a2b与-6ab2 |
| B、-x3y与2yx3 |
| C、2πR与R |
| D、35与53 |
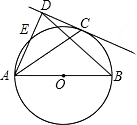 如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E.
如图,已知AB为⊙O直径,DC与⊙O相切于点C,AD⊥DC于D,AD交⊙O于E. 如图,AB∥CD,DF交AC于点F,DE=EF,求证:AE=EC.
如图,AB∥CD,DF交AC于点F,DE=EF,求证:AE=EC. 正方形ABCD边长为2,与函数x=
正方形ABCD边长为2,与函数x=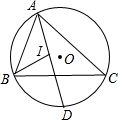 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.