题目内容
13. 如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.(1)求点C的坐标和直线l1的解析式;
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;
(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
分析 (1)根据平移的性质得到点C的坐标;把点B、C的坐标代入直线方程y=kx+b(k≠0)来求该直线方程;
(2)根据平移的性质得到点D的坐标,然后将其代入(1)中的函数解析式进行验证即可;
(3)根据点B的坐标求得直线l2的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答.
解答 解:(1)∵B(-3,3),将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,
∴-3+1=-2,3-2=1,
∴C的坐标为(-2,1),
设直线l1的解析式为y=kx+c,
∵点B、C在直线l1上,
∴代入得:$\left\{\begin{array}{l}{-3k+c=3}\\{-2k+c=1}\end{array}\right.$
解得:k=-2,c=-3,
∴直线l1的解析式为y=-2x-3;
(2)∵将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,C(-2,1),
∴-2-3=-5,1+6=7,
∴D的坐标为(-5,7),
代入y=-2x-3时,左边=右边,
即点D在直线l1上;
(3)把B的坐标代入y=x+b得:3=-3+b,
解得:b=6,
∴y=x+6,
∴E的坐标为(0,6),
∵直线y=-2x-3与y轴交于A点,
∴A的坐标为(0,-3),
∴AE=6+3=9,
∵B(-3,3),
∴△ABE的面积为$\frac{1}{2}$×9×|-3|=13.5.
点评 本题考查了用待定系数法求一次函数的解析式,平移的性质,一次函数图象上点的坐标特征,三角形的面积的应用,能理解每个点的求法是解此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3.已知∠A=45°,则∠A的补角等于( )
| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
18.当你乘车沿一条平坦的大道向前行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于它们前面那些矮一些的建筑物后面去了,这是因为( )
| A. | 汽车开的很快 | B. | 盲区减小 | C. | 盲区增大 | D. | 无法确定 |
2.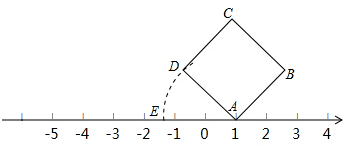 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )| A. | $-\sqrt{5}$ | B. | $1-\sqrt{5}$ | C. | $\frac{{-1-\sqrt{5}}}{2}$ | D. | $\frac{3}{2}-\sqrt{5}$ |
 如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.
如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.

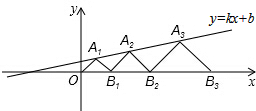 如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).