题目内容
2．在$\frac{1}{x}$、$\frac{1}{2}$、$\frac{{x}^{2}+1}{m}$、$\frac{3}{x+y}$中，分式的个数有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．
解答 解：在$\frac{1}{x}$、$\frac{1}{2}$、$\frac{{x}^{2}+1}{m}$、$\frac{3}{x+y}$中，分式有$\frac{1}{x}$、$\frac{{x}^{2}+1}{m}$、$\frac{3}{x+y}$，分式的个数有3个．
故选：B．
点评 本题主要考查分式的定义，分母中含有字母则是分式，如果不含有字母则不是分式．
练习册系列答案
相关题目
13．抛物线y=（x-1）2+t与x轴的两个交点之间的距离为4，则t的值是（ ）
| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
10．下列关于单项式-$\frac{x{y}^{3}}{2}$的说法中，正确的是（ ）
| A． | 系数是-$\frac{1}{2}$，次数是4 | B． | 系数是-$\frac{1}{2}$，次数是3 | ||
| C． | 系数是-2，次数是4 | D． | 系数是-2，次数是3 |
7．
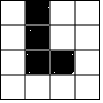在4×4的正方形网格中，已将图中的四个小正方形涂上阴影，若再从其余小正方形中任选一个也涂上阴影，是整个阴影部分组成的图形成轴对称图形，那么符合条件的小正方形共有（ ）
在4×4的正方形网格中，已将图中的四个小正方形涂上阴影，若再从其余小正方形中任选一个也涂上阴影，是整个阴影部分组成的图形成轴对称图形，那么符合条件的小正方形共有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
14．
如图，在平面直角坐标系中，点A是反比例函数y=$\frac{m}{x}$的图象上的一点，过点A作AB⊥x轴于点B，点C在y轴的负半轴上，连接AC，BC．若△ABC的面积为5，则m的值为（ ）
如图，在平面直角坐标系中，点A是反比例函数y=$\frac{m}{x}$的图象上的一点，过点A作AB⊥x轴于点B，点C在y轴的负半轴上，连接AC，BC．若△ABC的面积为5，则m的值为（ ）| A． | -10 | B． | 10 | C． | -5 | D． | 5 |
11．
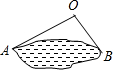如图所示，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B间的距离不可能是（ ）
如图所示，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B间的距离不可能是（ ）| A． | 5米 | B． | 15米 | C． | 10米 | D． | 20米 |