题目内容
12. 已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:
已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:①OE∥AC;
②两段劣弧$\widehat{DE}=\widehat{BE}$;
③FD与⊙O相切;
④S△BOE:S△BAC=1:4.
其中一定正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①只需运用等腰三角形性质就可得到∠OEB=∠ABC=∠ACB,从而可得OE∥AC;②连接OD,只需运用平行线的性质和等腰三角形的性质就可∠BOE=∠EOD,从而得到$\widehat{BE}=\widehat{DE}$;③易证△OBF≌△ODF,即可得到∠OBF=∠ODF.根据切线的性质可得∠OBF=90°,则有∠ODF=90°,即可得到DF与⊙O相切;④易证△BOE∽△BAC,根据相似三角形的性质即可得到$\frac{{S}_{△BOE}}{{S}_{△BAC}}$=$\frac{1}{4}$.
解答 解:①∵AB=AC,OB=OE,
∴∠ABC=∠ACB,∠OBE=∠OEB,
∴∠OEB=∠ACB,
∴OE∥AC.
故①正确;
②连接OD,如图.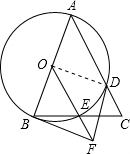 ∵OE∥AC,
∵OE∥AC,
∴∠BOE=∠OAD,∠EOD=∠ADO.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠BOE=∠EOD,
∴$\widehat{BE}=\widehat{DE}$.
故②正确;
③在△OBF和△ODF中,
$\left\{\begin{array}{l}{OB=OD}\\{∠BOF=∠DOF}\\{OF=OF}\end{array}\right.$,
∴△OBF≌△ODF,
∴∠OBF=∠ODF.
∵BF与⊙O相切于点B,
∴∠OBF=90°,
∴∠ODF=90°,
∴DF与⊙O相切.
故③正确;
④∵OC∥AC,
∴△BOE∽△BAC,
∴$\frac{{S}_{△BOE}}{{S}_{△BAC}}$=($\frac{BO}{BA}$)2=$\frac{1}{4}$.
故④正确.
故选D.
点评 本题主要考查了圆的切线的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、同圆或等圆中相等的圆心角所对的弧相等、等腰三角形的性质、平行线的性质等知识,难度不大,但覆盖的知识面比较广,是考查基础知识的一道好题.

| A. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$ |
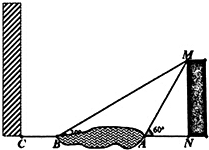 根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.
根据《城市居住区规划设计规范》要求,房屋之间的间距不得低于楼高1.2倍.某小区现已建好一幢高60米的住宅楼MN,该楼的背面(即图中楼房的右侧为正面,左侧为背面)有一座小区的景观湖,小丁在景观湖左右两侧各取一点观察该楼楼顶的M点,在A处测得点M的仰角为60°,在B处测得点M的仰角为30°,景观湖的左侧距离B点20米处有一点C,且C、B、A、N都在同一条直线上.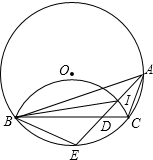 如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.
如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.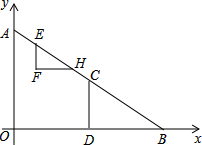 已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).
已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).