题目内容
6.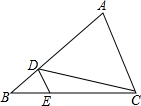 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△BAC=( )
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△BAC=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:25 |
分析 由S△BDE:S△CDE=1:4,于是得到BE:CE=1:4,从而推出BE:BC=1:5,根据DE∥AC,得到△BDE∽△CBA,然后根据相似三角形的性质得到结论.
解答 解:∵S△BDE:S△CDE=1:4,
∴BE:CE=1:4,
∴BE:BC=1:5,
∵DE∥AC,
∴△BDE∽△CBA,
∴S△BDE:S△BAC=($\frac{BE}{BC}$)2=$\frac{1}{25}$,
故选D.
点评 本题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答.

练习册系列答案
相关题目
15.下列说法正确的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
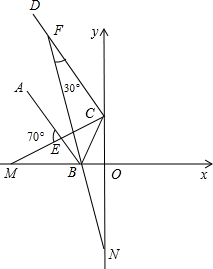 如图,在直角坐标系中,已知B(b,0),C(0,c),且|b+3|+(2c-8)2=0
如图,在直角坐标系中,已知B(b,0),C(0,c),且|b+3|+(2c-8)2=0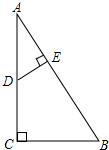 如图,在△ABC中,∠C=90°,∠B=60°,D是AC上一点,DE⊥AB于E,且CD=2,DE=1,则BC的长为$\frac{4\sqrt{3}}{3}$.
如图,在△ABC中,∠C=90°,∠B=60°,D是AC上一点,DE⊥AB于E,且CD=2,DE=1,则BC的长为$\frac{4\sqrt{3}}{3}$.