题目内容
15. 如图,锐角△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE相交于点O,且OB=OC.
如图,锐角△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE相交于点O,且OB=OC.(1)请你说明△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
分析 (1)根据OB=OC,得到∠OBC=∠OCB,再由BD⊥AC于点D,CE⊥AB于点E,进一步得到∠BCD=∠CBE,由等角对等边得到AB=AC,即可解答;
(2)欲证明O在∠BAC的平分线上,只需推知OE=OD即可.
解答 解:(1)∵OB=OC,
∴∠OBC=∠OCB,
∵BD⊥AC于点D,CE⊥AB于点E,
∴∠BCD=∠CBE,
∴AB=AC,
∴△ABC是等腰三角形;
(2)在△BEO与△CDO中,
$\left\{\begin{array}{l}{∠BOE=∠COD}\\{∠OEB=∠ODC=90°}\\{BE=CD}\end{array}\right.$,
∴△BEO≌△CDO(AAS),
∴OE=OD.
又∵BD⊥AC,CE⊥AB,
∴O在∠BAC的平分线上.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质和判定的应用,关键是推出△EBC≌△DCB,注意:等角对等边.

练习册系列答案
相关题目
3.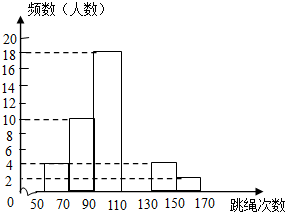 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
(1)a=10,b14.
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
 某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示),根据图表解答下列问题:| 组别 | 次数x | 频数(人数) |
| 第1组 | 50≤x<70 | 2 |
| 第2组 | 70≤x<90 | a |
| 第3组 | 90≤x<110 | 18 |
| 第4组 | 110≤x<130 | b |
| 第5组 | 130≤x<150 | 4 |
| 第6组 | 150≤x<170 | 2 |
(2)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则这50名男生中跳绳成绩为优秀的有多少人?优秀率为多少?
(3)若该校七年级入学时男生共有150人.请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
7.下列各数中最小的是( )
| A. | 23 | B. | -32 | C. | (-3)2 | D. | (-2)3 |
 如图,在四边形ABCD中,∠BAD=90°,AB=AD,CB=CD,AE⊥BC垂足为点E,(BE<EC),AE=6$\sqrt{2}$,CD=5$\sqrt{2}$,连接DE,则DE的长为2$\sqrt{17}$或8.
如图,在四边形ABCD中,∠BAD=90°,AB=AD,CB=CD,AE⊥BC垂足为点E,(BE<EC),AE=6$\sqrt{2}$,CD=5$\sqrt{2}$,连接DE,则DE的长为2$\sqrt{17}$或8. 如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.
如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.